题目内容
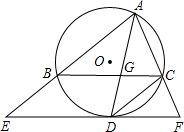 如图,已知⊙O为△ABC的外接圆,AD平分∠BAC交⊙O于D,过点D作EF∥BC分别交AB、AC延长线于点E、F.
如图,已知⊙O为△ABC的外接圆,AD平分∠BAC交⊙O于D,过点D作EF∥BC分别交AB、AC延长线于点E、F.(1)求证:EF为⊙O的切线;
(2)若EB=2,ED=4,求AB的长.
考点:切线的判定
专题:证明题
分析:(1)连结OD,根据角平分线定义得∠BAD=∠CAD,根据圆周角定理得
=
,则根据垂径定理的推论得OD⊥BC,由于BC∥EF,根据平行线的性质得OD⊥EF,于是可根据切线的性质可得到EF为⊙O的切线;
(2)根据平行线的性质由BC∥EF得到∠EDB=∠DBC,而
=
,根据圆周角定理得∠DBC=∠BAD,则可证明△EDB∽△EAD,然后根据相似比可计算出AE,再利用AB=AE-EB进行计算.
 |
| BD |
 |
| CD |
(2)根据平行线的性质由BC∥EF得到∠EDB=∠DBC,而
 |
| BD |
 |
| CD |
解答:(1)证明:连结OD,如图,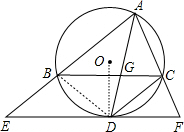
∵AD平分∠BAC交⊙O于D,
∴∠BAD=∠CAD,
∴
=
,
∴OD⊥BC,
∵BC∥EF,
∴OD⊥EF,
∴EF为⊙O的切线;
(2)解:∵BC∥EF,
∴∠EDB=∠DBC,
而
=
,
∴∠DBC=∠BAD,
∴∠EDB=∠EAD,
而∠DEB=∠AED,
∴△EDB∽△EAD,
∴
=
,即
=
,
∴AE=8
∴AB=AE-EB=6.

∵AD平分∠BAC交⊙O于D,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| CD |
∴OD⊥BC,
∵BC∥EF,
∴OD⊥EF,
∴EF为⊙O的切线;
(2)解:∵BC∥EF,
∴∠EDB=∠DBC,
而
 |
| BD |
 |
| CD |
∴∠DBC=∠BAD,
∴∠EDB=∠EAD,
而∠DEB=∠AED,
∴△EDB∽△EAD,
∴
| ED |
| EA |
| EB |
| ED |
| 4 |
| AE |
| 2 |
| 4 |
∴AE=8
∴AB=AE-EB=6.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质、圆周角定理和垂径定理.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
下列四个图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,DE∥BC,∠B=52°,沿DE折叠,点A落在三角形所在的平面内的点为A,则∠BDA的度数为
如图,在△ABC中,DE∥BC,∠B=52°,沿DE折叠,点A落在三角形所在的平面内的点为A,则∠BDA的度数为
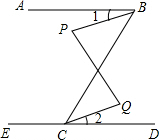 如图,已知∠ABC=63°,∠ECB=117°,∠P=∠Q.
如图,已知∠ABC=63°,∠ECB=117°,∠P=∠Q.