题目内容
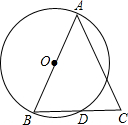 如图,△ABC的顶点A、B在⊙O上,边BC与⊙O 交于点D.①AB=AC;②BD=DC;③AB是⊙O的直径.此三个条件中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②?③;①③?②;②③?①.
如图,△ABC的顶点A、B在⊙O上,边BC与⊙O 交于点D.①AB=AC;②BD=DC;③AB是⊙O的直径.此三个条件中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②?③;①③?②;②③?①.(1)以上三个命题是真命题的为(直接作答)
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
考点:命题与定理,圆周角定理
专题:
分析:(1)三个命题都是真命题;
(2)选①③?②进行证明,根据圆周角定理由AB为直径得到∠ADB=90°,即AD⊥BC,然后根据等腰三角形的性质易得BD=CD.
(2)选①③?②进行证明,根据圆周角定理由AB为直径得到∠ADB=90°,即AD⊥BC,然后根据等腰三角形的性质易得BD=CD.
解答:解:(1)答案为①②?③;①③?②;②③?①.
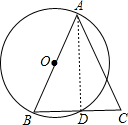 (2)①③?②.证明如下:
(2)①③?②.证明如下:
连结AD,
∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD.
 (2)①③?②.证明如下:
(2)①③?②.证明如下:连结AD,
∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD.
点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式,有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了圆周角定理.

练习册系列答案
相关题目
已知二次函数y=x2+2x+3,当0≤x≤3时,下列说法正确的是( )
| A、有最小值2,最大值18 |
| B、有最小值3,最大值18 |
| C、有最小值0,最大值3 |
| D、有最小值2,最大值12 |
 如图,∠AOB的平分线上一点P到OA的距离为5,Q是OB上任意一点,则PQ的范围是
如图,∠AOB的平分线上一点P到OA的距离为5,Q是OB上任意一点,则PQ的范围是 如图,在⊙O的内接四边形ABCD中,AB=AD,∠BCD=140°.若点E在
如图,在⊙O的内接四边形ABCD中,AB=AD,∠BCD=140°.若点E在
 如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠AOE=
如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠AOE=