题目内容
【阅读】|5-2|表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|可以看做|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
【探索】
(1)若|x-2|=5,则x= ;
(2)利用数轴,找出所有符合条件的整数x,使x所表示的点到2和-1所对应的点的距离之和为3.
(3)由以上探索猜想,对于任意有理数x,|x-2|+|x+3|是否有最小值?如果有,写出最小值;如果没有,说明理由.
【探索】
(1)若|x-2|=5,则x=
(2)利用数轴,找出所有符合条件的整数x,使x所表示的点到2和-1所对应的点的距离之和为3.
(3)由以上探索猜想,对于任意有理数x,|x-2|+|x+3|是否有最小值?如果有,写出最小值;如果没有,说明理由.
考点:绝对值,数轴
专题:
分析:(1)|x-2|可以理解为x与2两数在数轴上所对应的两点之间的距离,根据|x-2|=5即可求得x的值;
(2)计算|x-2|+|x+1|=3,求得x的取值范围即可解题;
(3)|x-2|+|x+3|可以理解为数轴上一个点到2和-3的距离,即可解题.
(2)计算|x-2|+|x+1|=3,求得x的取值范围即可解题;
(3)|x-2|+|x+3|可以理解为数轴上一个点到2和-3的距离,即可解题.
解答:解:|x-2|可以理解为x与2两数在数轴上所对应的两点之间的距离,
到2的距离为5的数字有7和-3,
故答案为7或-3;
(2)|x-2|+|x+1|=3,
当x<-1时,|x-2|+|x+1|=2-x-1-x=3-2x=3,x=0(不符合题意舍去);
当1-≤x≤2时,|x-2|+|x+1|=2-x+x+1=3,
当x>2时,|x-2|+|x+1|=x-2+x+1=2x-1=3,x=2(不符合题意舍去);
综上所述,当1-≤x≤2时,x所表示的点到2和-1所对应的点的距离之和为3;
(3)|x-2|+|x+3|可以理解为数轴上一个点到2和-3的距离,
求证方法和(2)相同,故有最小值为5.
到2的距离为5的数字有7和-3,
故答案为7或-3;
(2)|x-2|+|x+1|=3,
当x<-1时,|x-2|+|x+1|=2-x-1-x=3-2x=3,x=0(不符合题意舍去);
当1-≤x≤2时,|x-2|+|x+1|=2-x+x+1=3,
当x>2时,|x-2|+|x+1|=x-2+x+1=2x-1=3,x=2(不符合题意舍去);
综上所述,当1-≤x≤2时,x所表示的点到2和-1所对应的点的距离之和为3;
(3)|x-2|+|x+3|可以理解为数轴上一个点到2和-3的距离,
求证方法和(2)相同,故有最小值为5.
点评:本题考查了绝对值的计算,考查了绝对值的定义.本题属于基础题,牢记绝对值定义是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
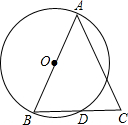 如图,△ABC的顶点A、B在⊙O上,边BC与⊙O 交于点D.①AB=AC;②BD=DC;③AB是⊙O的直径.此三个条件中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②?③;①③?②;②③?①.
如图,△ABC的顶点A、B在⊙O上,边BC与⊙O 交于点D.①AB=AC;②BD=DC;③AB是⊙O的直径.此三个条件中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②?③;①③?②;②③?①. 甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜,请你解决下列问题:
甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜,请你解决下列问题: 用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.
用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形. 如图,BD,CE分别为△ABC的两条高线,F为BC的中点,则△DEF是
如图,BD,CE分别为△ABC的两条高线,F为BC的中点,则△DEF是