题目内容
7.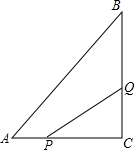 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得四边形APQB的面积等于△ABC的面积的四分之一?若存在,求出运动的时间;若不存在,说明理由.
分析 (1)设x秒钟后,可使△PCQ的面积为8平方厘米,用x表示出△PCQ的边长,根据面积是8可列方程求解.
(2)假设y秒时四边形APQB的面积等于△ABC的面积的$\frac{1}{4}$,列出方程看看解的情况,可知是否有解.
解答 解:(1)设x秒钟后,可使△PCQ的面积为8平方厘米,由题意得:
$\frac{1}{2}$(6-x)•2x=8,
x=2或x=4,
当2秒或4秒时,面积可为8平方厘米;
(2)不存在.
理由:设y秒时,四边形APQB的面积等于△ABC的面积的$\frac{1}{4}$,
则△QPC的面积是△ABC的面积的$\frac{3}{4}$,
由题意得:
$\frac{1}{2}$(6-y)•2y=$\frac{3}{4}$×$\frac{1}{2}$×6×8
y2-6y+18=0.
△=36-4×18=-36<0,
方程无解,所以不存在.
点评 本题考查了一元二次方程的应用,三角形的面积公式的求法和一元二次方程的解的情况,表示出△PCQ的面积是解题关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
12.如图所示,将一个圆依次二等分、三等分、四等分、五等分…,并按图中规律在半径上摆放黑色棋子,则第一幅图中有5个棋子,第二幅图中有10个棋子,第三幅图中有17个棋子,第四幅图中有26个棋子,依此规律,则第6幅图中所含棋子数目为( )


| A. | 51 | B. | 50 | C. | 49 | D. | 48 |
16.下列图形中不是轴对称图形的是( )
| A. | 等腰三角形 | B. | 平行四边形 | C. | 正五边形 | D. | 线段 |
17.下面各式中,去括号正确的是( )
| A. | a-(b+c)=a-b-c | B. | a-(b+c)=a+b-c | C. | a-(b+c)=a+b+c | D. | a-(b+c)=a-b+c |
 已知数a、b的对应点在数轴上的位置如图所示,则a-3<b-3.
已知数a、b的对应点在数轴上的位置如图所示,则a-3<b-3.
 如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.
如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C. 如图,点O为优弧ACB所在圆的圆心,∠AOC=100°,点D在AB的延长线上,BD=BC,则∠D=25°.
如图,点O为优弧ACB所在圆的圆心,∠AOC=100°,点D在AB的延长线上,BD=BC,则∠D=25°.