题目内容
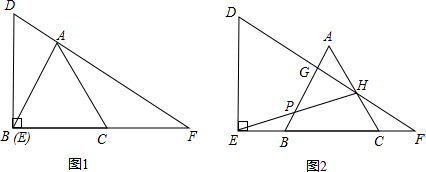
18.已知△ABC是等边三角形,AB=6,将一块含有30°角的直角三角板DEF如图所示放置,让等边△ABC向右平移(BC只能在EF上移动).如图1,当点E与点B重合时,点A恰好落在三角板DEF的斜边DF上.(1)若点C平移到与点F重合,求等边△ABC平移的距离;
(2)在等边△ABC向右平移的过程中,AB,AC与三角板斜边的交点分别为G,H,连接EH交AB于点P,如图2.
①求证:EB=AH;
②若∠HEF=30°,求EH的长;
③判断PG的长度在等边△ABC平移的过程中是否会发生变化?如果不变,请求出PG的长;如果变化,请说明理由.
分析 (1)就是刚开始时C点与F的距离;
(2)①作EM⊥DF于点M,EN⊥AB于点N,证明△EBN≌△HAG即可;
②此时HEF是等腰三角形,作HP⊥EF于点P,由(1)知,EF=2AB,从而PE=AB=6,EH自然求出;
③由于前面已经证明了△EBN≌△HAG,从而有GH=EN,则△ENP≌△HGP,PG=NP=$\frac{1}{2}$AB.
解答 解:(1)等边△ABC未平移时,如图1,
∵∠ABC=60°,BD⊥BF,
∴∠DBA=30°,
∵∠BDF=60°,
∴BA⊥DF,
∴2AB=BF=BC+CF,
∵AB=BC,
∴CF=AB=6,
即:点C平移到与点F重合时,等边△ABC平移的距离为6;
(2)
①作EM⊥DF于点M,EN⊥AB于点N,如图2,
由(1)知AB⊥DF,
∴MENG是矩形,
∴GN=EM=AB,
∵∠ACB=60°,∠DFE=30°,
∴∠CHF=30°,
∴∠AHG=30°,
∵EN∥DF,
∴∠BEN=30°=∠AHG,
∵AG+GB=AB,
BN+GB=NG=AB,
∴BN=AG,
在△EBN和△HAG中,
$\left\{\begin{array}{l}{∠BEN=∠AHG}\\{∠ENB=∠AHG}\\{AG=BN}\end{array}\right.$,
∴△EBN≌△HAG(AAS),
∴EB=AH;
②如图3,作HP⊥EF于点P,
∵∠HEF=30°=∠HFE,
∴PE=PF,
由(1)知EF=2AB=12,
∴PE=6,
∴PH=$2\sqrt{3}$,
∴EH=4$\sqrt{3}$;
③不变.如图2,
∵△EBN≌△HAG,
∴GH=NE,
在△ENP和△HGP中,
$\left\{\begin{array}{l}{∠ENP=∠HGP}\\{∠EPN=∠HPG}\\{EN=HG}\end{array}\right.$,
∴△ENP≌△HGP(AAS),
∴GP=NP=$\frac{1}{2}$NG=$\frac{1}{2}AB$=3.
点评 本题考查了等边三角形的性质、含30度的直角三角形的性质、矩形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质等知识点,综合性较强,有一定难度.清楚AB等于点E到DF的距离且在平移过程中始终与DF垂直是作出辅助线的突破口和关键.

| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -4 |
(2)在第几次纪录时距A地最远?
(3)若汽车行驶每千米耗油0.2升,问从A地出发,检修结束后再回到A地共耗油多少升?
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
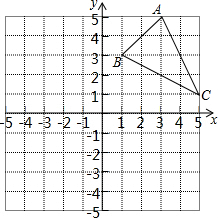 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).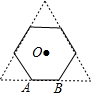 如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.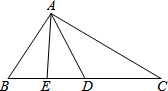 如图,AE是△ABD的中线AB=CD=BD.
如图,AE是△ABD的中线AB=CD=BD.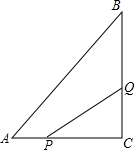 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.