题目内容
2. 如图,点O为优弧ACB所在圆的圆心,∠AOC=100°,点D在AB的延长线上,BD=BC,则∠D=25°.
如图,点O为优弧ACB所在圆的圆心,∠AOC=100°,点D在AB的延长线上,BD=BC,则∠D=25°.
分析 先根据等腰三角形的性质得到∠BCD=∠D,再根据三角形外角性质得∠ABC=∠BCD+∠D=2∠D,然后根据圆周角定理得到∠ABC的度数,进而可得出结论.
解答 解:∵:∵BC=BD,
∴∠BCD=∠D,
∴∠ABC=∠BCD+∠D=2∠D,
∵∠ABC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×100°=50°,
∴∠D=$\frac{1}{2}$∠ABC=25°.
故答案为:25.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
10.若关于x的一元二次方程kx2-6x+3=0有两个实数根,则k的取值范围中,非负整数值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
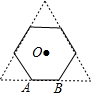 如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
如图,正三角形的边长为6cm,剪去三个角后成一个正六边形. 一次函数y1=x-2与二次函数y2=ax2+bx+c的图象交于A(2,m)、B(n,3)两点,且抛物线的对称轴为直线x=3.
一次函数y1=x-2与二次函数y2=ax2+bx+c的图象交于A(2,m)、B(n,3)两点,且抛物线的对称轴为直线x=3.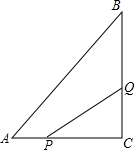 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.