题目内容
15. 如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.
如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.(1)求点m的值和二次函数的解析式;
(2)求二次函数的顶点坐标和对称轴;
(3)请直接写出当y1<y2时,自变量的取值范围.
分析 (1)把A的坐标代入一次函数解析式即可求得m的值,利用待定系数法即可求得二次函数的解析式;
(2)利用配方法即可求得顶点坐标和对称轴;
(3)求得A和B的横坐标,当y1<y2时,y2的图象在上边,据此求得自变量的取值范围.
解答 解:(1)把(-1,0)代入y1=-x+m得1+m=0,
解得:m=-1;
根据题意得:$\left\{\begin{array}{l}{a-b-3=0}\\{4a+2b-3=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
则二次函数的解析式是y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4.
则顶点坐标是(1,-4),对称轴是x=1;
(3)一次函数的解析式是y=-x-1,
根据题意得:x2-2x-3=-x-1,即x2-x-2=0,
解得:x1=-1,x2=2.
则A和B的横坐标分别是-1和2.
则当y1<y2时,自变量的取值范围是:x<-1或x>2.
点评 本题考查了待定系数法求函数解析式,利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,利用交点直观求解.

练习册系列答案
相关题目
10.若关于x的一元二次方程kx2-6x+3=0有两个实数根,则k的取值范围中,非负整数值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.某商品经过连续两次降价后售价为256元,原售价289元.设平均每次降价的百分率为x,则下面所列方程中正确的是( )
| A. | 289(1-x)2=256 | B. | 256(1-x)2=289 | C. | 289(1-2x)=256 | D. | 256(1-2x)=289 |
4.下列四个式子中,计算结果最小的是( )
| A. | (-3-2)2 | B. | (-3)×(-2)2 | C. | -32÷(-2)2 | D. | -23-32 |
 如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是10.
如图,△ABC中,BC=10,DH为AB的中垂线,EF垂直平分AC,则△ADE的周长是10.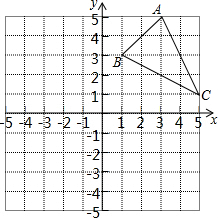 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).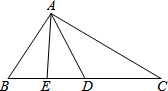 如图,AE是△ABD的中线AB=CD=BD.
如图,AE是△ABD的中线AB=CD=BD.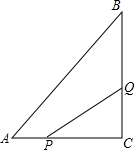 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.