题目内容
7．比较$\sqrt{5}$，$\root{3}{7}$，2的大小，正确的是（ ）| A． | $2＜\sqrt{5}＜\root{3}{7}$ | B． | $2＜\root{3}{7}＜\sqrt{5}$ | C． | $\root{3}{7}＜2＜\sqrt{5}$ | D． | $\sqrt{5}＜\root{3}{7}＜2$ |
分析 首先利用算术平方根的定义得出$\sqrt{5}$＞2，再利用立方根的定义得出$\root{3}{7}$＜2，进而得出答案．
解答 解：∵$\sqrt{4}$＜$\sqrt{5}$＜$\sqrt{9}$，
∴$\sqrt{5}$＞2，
∵$\root{3}{7}$＜$\root{3}{8}$=2，
∴$\root{3}{7}$＜2，
∴$\sqrt{5}$，$\root{3}{7}$，2的大小关系为：$\root{3}{7}$＜2＜$\sqrt{5}$．
故选：C．
点评 此题主要考查了实数大小比较，正确掌握算术平方根以及立方根的定义是解题关键．
练习册系列答案
相关题目
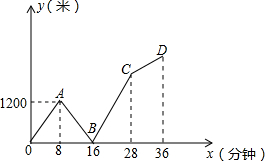小明的爸爸和小明旱晨同时从家出发，以各自的速度匀速步行上班和上学，爸爸前往位于家正东方的公司，小明前往位于家正西方的学校，爸爸到达公司后发现小明的数学作业在自己的公文包里，于是立即跑步去小明，终于在途中追上了小明把作业给了他，然后再以先前的速度步行再回公司（途中给作业的时间忽略不计）．结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟．如图是两人之间的距离y（米）与他们从家出发的时间x（分钟）的函数关系图，则小明家与学校相距1800米．
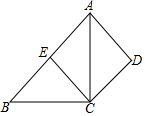如图，在△ABC中，∠ACB=90°，E是AB的中点，AD∥EC，CD∥AB，试判断四边形ADCE的形状，并证明你的结论．
12．二次函数y=（x-3）2-2的图象上最低点的坐标是（ ）
| A． | （-3，-2） | B． | （3，-2） | C． | （-3，2） | D． | （3，2） |
19．单项式$\frac{1}{2}$x2y3的系数和次数分别是（ ）
| A． | 1，2 | B． | 2，3 | C． | $\frac{1}{2}$，5 | D． | $\frac{1}{2}$，2 |
16．
有理数a，b在数轴上的位置如图所示，则|a+b|-2|a|化简的结果为（ ）
有理数a，b在数轴上的位置如图所示，则|a+b|-2|a|化简的结果为（ ）| A． | b-a | B． | 3a+b | C． | a-b | D． | -3a-b |
17．把一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷2次，若两次正面朝上的编号分别为m、n，则二次函数y=x2-mx+n的图象与x轴有两个不同交点的概率是（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{4}{9}$ | C． | $\frac{17}{36}$ | D． | $\frac{1}{2}$ |