题目内容
6.如图1,方格纸的单位正方形边长为1,点A、B、C、D刚好在方格纸的格点上.(1)将三角形ABC进行平移,使点A平移至点D的位置上,请画出平移后的三角形DEF;
(2)若以点B为原点建立平面直角坐标系,请写出点F的坐标:(1,-4);
(3)如图2,将三角形ABC以BC边为折痕折叠一次后,形成四边形ABEC,写出四边形ABEC的面积:6.
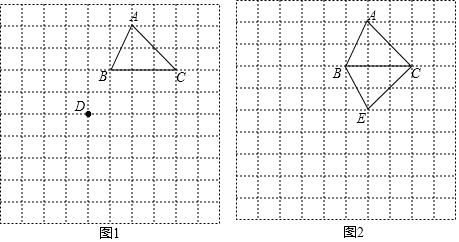
分析 (1)将△ABC先向下平移4个单位长度,再向左平移2个单位长度即可;
(2)以点B为原点建立平面直角坐标系,则点F在第四象限内,据此可得点F的坐标;
(3)依据四边形ABEC的面积=2×△ABC的面积,进行计算即可.
解答 解:(1)如图1所示,三角形DEF即为所求;
(2)若以点B为原点建立平面直角坐标系,则点F的坐标为(1,-4),
故答案为:(1,-4);
(3)如图2所示,四边形ABEC的面积=2×△ABC的面积=2×$\frac{1}{2}$×3×2=6.
故答案为:6.
点评 本题主要考查了利用平移变换进行作图以及轴对称性质的运用,解题时注意:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
16.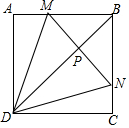 如图,在正方形ABCD中,点M、N分别在AB、BC上,△DMN是等边三角形,连接BD交MN于P,给出下列结论:①AM=CN;②∠CDN=15°;③BD垂直平分MN;④AM+CN=MN,其中结论正确的共有( )
如图,在正方形ABCD中,点M、N分别在AB、BC上,△DMN是等边三角形,连接BD交MN于P,给出下列结论:①AM=CN;②∠CDN=15°;③BD垂直平分MN;④AM+CN=MN,其中结论正确的共有( )
 如图,在正方形ABCD中,点M、N分别在AB、BC上,△DMN是等边三角形,连接BD交MN于P,给出下列结论:①AM=CN;②∠CDN=15°;③BD垂直平分MN;④AM+CN=MN,其中结论正确的共有( )
如图,在正方形ABCD中,点M、N分别在AB、BC上,△DMN是等边三角形,连接BD交MN于P,给出下列结论:①AM=CN;②∠CDN=15°;③BD垂直平分MN;④AM+CN=MN,其中结论正确的共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.顺次连接矩形各边中点所得的四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 梯形 | D. | 以上都不对 |
1.对于一次函数y=2x+4,下列结论中正确的是( )
①若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,则y1<y2.
②函数的图象不经过第四象限.
③函数的图象与x轴的交点坐标是(0,4).
④函数的图象向下平移4个单位长度得y=2x的图象.
①若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,则y1<y2.
②函数的图象不经过第四象限.
③函数的图象与x轴的交点坐标是(0,4).
④函数的图象向下平移4个单位长度得y=2x的图象.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.学校准备从甲、乙、丙、丁四个小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数(分)及方差如下表所示:
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1.1 | 1.3 | 1.1 | 1.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
18.下列各图中,∠1与∠2一定是互补关系的是( )
| A. |  | B. |  | C. |  | D. |  |
15.用代入法解方程组$\left\{\begin{array}{l}{2x-y=1①}\\{3y+4x=2②}\end{array}\right.$时,将①变形正确的是( )
| A. | y=2x+1 | B. | y=1-2x | C. | y=2x-1 | D. | y=-2x-1 |
16. 如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )
如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )
 如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )
如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )| A. | 35° | B. | 35°或50° | C. | 25°或70° | D. | 50°或70° |