题目内容
2.一次数学课上,老师让大家在一张长12cm、宽5cm的矩形纸片内,折出一个菱形.甲同学按照取两组对边中点的方法折出菱形EFGH(方案一),乙同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(方案二),请你通过计算,比较这两种方案中,折出的菱形面积较大的方案是( )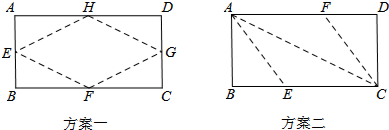
| A. | 方案一 | B. | 方案二 | ||
| C. | 两个方案一样 | D. | 无法通过计算来比较大小 |
分析 根据折叠方法,分别求得甲同学和乙同学的折法中的菱形面积,比较即可求得答案.
解答 解:(方案一)S菱形=S矩形-4S△AEH=12×5-4×$\frac{1}{2}$×6×$\frac{5}{2}$=30(cm2).
(方案二)设BE=x,则CE=12-x,
∴AE=$\sqrt{B{E}^{2}+A{B}^{2}}$.
∵四边形AECF是菱形,则AE2=CE2,
∴25+x2=(12-x)2.
∴x=$\frac{119}{24}$.
∴S菱形=S矩形-2S△ABE=12×5-2×$\frac{1}{2}$×5×$\frac{119}{24}$≈35.21(cm2).
经比较可知,(方案二)乙同学所折的菱形面积较大.
故选B.
点评 此题考查了菱形的性质、勾股定理以及矩形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
12.下列成语所描述的事件是必然事件的是( )
| A. | 水涨船高 | B. | 守株待兔 | C. | 水中捞月 | D. | 画饼充饥 |
14.顺次连接矩形各边中点所得的四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 梯形 | D. | 以上都不对 |
11.学校准备从甲、乙、丙、丁四个小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数(分)及方差如下表所示:
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1.1 | 1.3 | 1.1 | 1.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
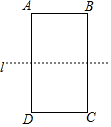 如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个.
如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个. 母亲节过后,永川区某校在本校学生中做了一次抽样调查,并把调查结果分成三种类型:A.已知道哪一天是母亲节的;B.知道但没有任何行动的;C.知道并问候母亲的.如图是根据调查结果绘制的统计图(部分),根据图中提供的信息,回答下列问题:
母亲节过后,永川区某校在本校学生中做了一次抽样调查,并把调查结果分成三种类型:A.已知道哪一天是母亲节的;B.知道但没有任何行动的;C.知道并问候母亲的.如图是根据调查结果绘制的统计图(部分),根据图中提供的信息,回答下列问题: