题目内容
 如图,直线y=-
如图,直线y=-
| ||
| 3 |
(1)求三角形ABC的面积S△ABC;
(2)求点C的坐标;
(3)证明不论a取任何实数,△BOP的面积是一个常数.
考点:一次函数综合题,全等三角形的判定与性质,勾股定理
专题:综合题
分析:(1)由题可得点A、B的坐标,从而得到OA、OB的长,根据勾股定理可求出AB,就可求出等腰直角△ABC的面积;
(2)过点C作CH⊥x轴于点H,如图1,易证△AOB≌△CHA,从而得到AH、CH,就可得到点C的坐标;
(3)过点P作PE⊥y轴于点E,如图2,由P(1,a)可得PE=1,从而得到△BOP的面积是一个常数.
(2)过点C作CH⊥x轴于点H,如图1,易证△AOB≌△CHA,从而得到AH、CH,就可得到点C的坐标;
(3)过点P作PE⊥y轴于点E,如图2,由P(1,a)可得PE=1,从而得到△BOP的面积是一个常数.
解答:解:(1)∵直线y=-
x+1与x轴,y轴分别交于点A、B,
∴点A的坐标为(
,0),点B的坐标为(0,1),
∴OA=
,OB=1,
∵∠AOB=90°,
∴AB=
=2.
∴AC=AB=2,
∵∠BAC=90°,
∴S△ABC=
AB•AC=2;
(2)过点C作CH⊥x轴于点H,如图1,

则∠AHC=90°.
∴∠AOB=∠BAC=∠AHC=90°,
∴∠OAB=180°-90°-∠HAC=90°-∠HAC=∠HCA.
在△AOB和△CHA中,
,
∴△AOB≌△CHA(AAS),
∴AO=CH=
,OB=HA=1,
∴OH=OA+AH=
+1,
∴点C的坐标为(
+1,
);
(3)证明:过点P作PE⊥y轴于点E,如图2.

∵P(1,a),
∴PE=1,
∴S△BOP=
OB•PE=
×1×1=
,
∴不论a取任何实数,△BOP的面积都是一个常数.
| ||
| 3 |
∴点A的坐标为(
| 3 |
∴OA=
| 3 |
∵∠AOB=90°,
∴AB=
| OA2+OB2 |
∴AC=AB=2,
∵∠BAC=90°,
∴S△ABC=
| 1 |
| 2 |
(2)过点C作CH⊥x轴于点H,如图1,

则∠AHC=90°.
∴∠AOB=∠BAC=∠AHC=90°,
∴∠OAB=180°-90°-∠HAC=90°-∠HAC=∠HCA.
在△AOB和△CHA中,
|
∴△AOB≌△CHA(AAS),
∴AO=CH=
| 3 |
∴OH=OA+AH=
| 3 |
∴点C的坐标为(
| 3 |
| 3 |
(3)证明:过点P作PE⊥y轴于点E,如图2.

∵P(1,a),
∴PE=1,
∴S△BOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴不论a取任何实数,△BOP的面积都是一个常数.
点评:本题主要考查了一次函数图象上点的坐标特征、全等三角形的判定与性质、勾股定理、三角形的面积公式等知识,构造全等三角形是解决第(2)小题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
若抛物线y=x2-2x+c与y轴的交点为(0,-3),则该抛物线与x轴的交点是( )
| A、(-1,0)和(0,3) |
| B、(0,-1)和(3,0) |
| C、(-1,0)和(3,0) |
| D、(0,-1)和(0,3) |
已知⊙O的半径为3,线段OP的长度为2,则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
 如图,每个小正方形的边长都等于1,则△ABC的外心坐标是
如图,每个小正方形的边长都等于1,则△ABC的外心坐标是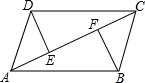 如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB, 如图,半径为30cm的转动轮转过240°时,传送带上的物体A平移的距离为
如图,半径为30cm的转动轮转过240°时,传送带上的物体A平移的距离为