题目内容
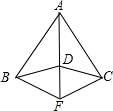 已知:如图,AB=AC,DB=DC.F是AD的延长线上一点.
已知:如图,AB=AC,DB=DC.F是AD的延长线上一点.求证:(1)∠ABD=∠ACD;
(2)BF=CF.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据SSS推出△BAD≌△CAD,根据全等三角形的性质得出即可;
(2)根据SAS推出△BAF≌△CAF,根据全等三角形的性质得出即可.
(2)根据SAS推出△BAF≌△CAF,根据全等三角形的性质得出即可.
解答:证明:(1)∵在△BAD和△CAD中
∴△BAD≌△CAD,
∴∠ABD=∠ACD;
(2)∵在△BAF和△CAF中
∴△BAF≌△CAF,
∴BF=CF.
|
∴△BAD≌△CAD,
∴∠ABD=∠ACD;
(2)∵在△BAF和△CAF中
|
∴△BAF≌△CAF,
∴BF=CF.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知⊙O的半径为3,线段OP的长度为2,则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
等边三角形的对称轴有( )
| A、1条 | B、1条或3条 |
| C、3条 | D、4条 |
 如图,每个小正方形的边长都等于1,则△ABC的外心坐标是
如图,每个小正方形的边长都等于1,则△ABC的外心坐标是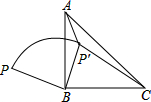 如图,P是等腰Rt△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:
如图,P是等腰Rt△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1: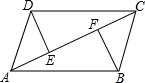 如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,