题目内容
 如图,BD是圆O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.
如图,BD是圆O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.(1)求证:AB2=AD•AE;
(2)若AE=2,ED=4,求AB的长;
(3)在(2)的条件下,直线FA为⊙O相切吗?为什么?
考点:圆的综合题
专题:综合题
分析:(1)先由AB=AC得到∠ABC=∠C,再根据圆周角定理得∠C=∠D,然后根据相似三角形的判定方法得到△ABE∽△ADB,再利用相似比和比例的性质即可得到结论;
(2)利用(1)的结论计算;
(3)先在Rt△ABD中利用勾股定理计算出BD=4
,则OB=OA=2
,于是可判断△OAB为等边三角形,得到∠ABD=∠BAO=60°,再计算出∠BAF=30°,由此得到∠OAF=∠BAO+∠BAF=90°,然后根据切线的判定定理得直线FA与⊙O相切.
(2)利用(1)的结论计算;
(3)先在Rt△ABD中利用勾股定理计算出BD=4
| 3 |
| 3 |
解答:(1)证明:∵AB=AC,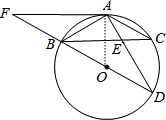
∴∠ABC=∠C,
而∠C=∠D,
∴∠D=∠ABC,
而∠EAB=∠BAD,
∴△ABE∽△ADB,
∴
=
,
∴AB2=AD•AE;
(2)解:连接OA,如图,
∵AB2=AD•AE,
∴AB2=2•(2+4),
∴AB=2
;
(3)解:直线FA与⊙O相切.理由如下:
在Rt△ABD中,∵AB=2
,AD=6,
∴BD=
=4
,
∴OB=OA=2
,
∴△OAB为等边三角形,
∴∠ABD=∠BAO=60°,
∵BO=BF,
∴BF=AB,
∴∠F=∠BAF,
∴∠BAF=30°,
∴∠OAF=∠BAO+∠BAF=60°+30°=90°,
∴OA⊥AF,
∴直线FA与⊙O相切.

∴∠ABC=∠C,
而∠C=∠D,
∴∠D=∠ABC,
而∠EAB=∠BAD,
∴△ABE∽△ADB,
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AD•AE;
(2)解:连接OA,如图,
∵AB2=AD•AE,
∴AB2=2•(2+4),
∴AB=2
| 3 |
(3)解:直线FA与⊙O相切.理由如下:
在Rt△ABD中,∵AB=2
| 3 |
∴BD=
| AB2+AD2 |
| 3 |
∴OB=OA=2
| 3 |
∴△OAB为等边三角形,
∴∠ABD=∠BAO=60°,
∵BO=BF,
∴BF=AB,
∴∠F=∠BAF,
∴∠BAF=30°,
∴∠OAF=∠BAO+∠BAF=60°+30°=90°,
∴OA⊥AF,
∴直线FA与⊙O相切.
点评:本题考查了圆的综合题:熟练掌握圆周角定理、切线的判定定理和相似三角形的判定与性质;会运用相似比和勾股定理进行几何计算.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知点P(6,-6),Q(-6,-6),则直线PQ( )
| A、平行于x轴 |
| B、平行于y轴 |
| C、不平行于任何坐标轴 |
| D、不能确定 |
等边三角形的对称轴有( )
| A、1条 | B、1条或3条 |
| C、3条 | D、4条 |
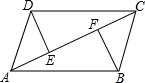 如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB, 如图,半径为30cm的转动轮转过240°时,传送带上的物体A平移的距离为
如图,半径为30cm的转动轮转过240°时,传送带上的物体A平移的距离为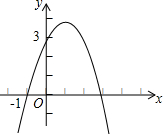 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)