Question

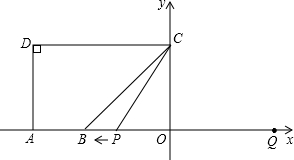如图，点A（-10，0），B（-6，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB，∠CDA=90°．点P从点Q（8，0）出发，沿x轴向左以每秒1个单位长的速度向点A匀速运动，运动时间为t秒．
（1）求点C的坐标；
（2）当∠BCP=15°，求t的值；
（3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边ABCD的边（或边所在的直线）相切时，求t的值．

Answer 1

考点：圆的综合题

专题：

分析：（1）由点C在y轴的正半轴上，∠CBO=45°，易得∠BCO=∠CBO=45°，则可求得OC=OB=6，即可求得答案；
（2）分别从当点P在点B右侧与左侧时去分析求解，借助于三角函数的知识，即可求得答案；
（3）分别从当⊙P与BC相切于点C时，则∠BCP=90°，当⊙P与CD相切于点C时，有PC⊥CD，即点P与点O重合，当⊙P与AD相切时，由题意得：∠DAO=90°，去分析求解即可求得答案．

解答：解：（1）∵∠BOC=90°，∠CBO=45°，
∴∠BCO=∠CBO=45°，
∵B（-6，0），
∴OC=OB=6，
 又∵点C在y轴的正半轴上，?
∴C（0，6）；

（2）①当点P在点B右侧时，
∵∠BCO=45°，∠BCP=15°，
∴∠POC=30°，
∴OP=OC•tan∠POC=6×

3

3

=2

3

，
∴t₁=8+2

3

，
②当点P在点B左侧时，
∵∠BCO=45°，∠BCP=15°，
∴∠POC=60°，
∴OP=OC•tan∠POC=6×

3

=6

3

，
∴t₂=8+6

3

，
，综上所述：t的值为8+2

3

或8+6

3

．

（3）由题意知：若⊙P与四边形ABCD的边都相切，有以下三种情况：
①当⊙P与BC相切于点C时，则∠BCP=90°，
∵∠OCB=45°，
∴∠OCP=45°，
∴OP=OB=6，
此时t₁=8-6=2；
②当⊙P与CD相切于点C时，有PC⊥CD，即点P与点O重合，?
此时t₂=8；
③当⊙P与AD相切时，由题意得：∠DAO=90°，
∴点A为切点，
设OP=x，则PA=PC=10-x，
∴6²+x²=（10-x）²，
∴x=3.2，
∴OP=3.2，
∴t₃=8+3.2=11.2；
综上所述：t的值为2或8或11.2．

点评：此题考查了切线的性质、矩形的性质、直角三角形的性质以及三角函数等知识．此题难度较大，注意掌握数形结合思想、分类讨论思想与方程思想的应用．