题目内容
19.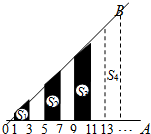 如图,∠AOB=45°,过0A上到点O的距离分别为1,3,5,7,9,11,L的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,L.观察图中的规律,求出第11个黑色梯形的面积S11=84.
如图,∠AOB=45°,过0A上到点O的距离分别为1,3,5,7,9,11,L的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,L.观察图中的规律,求出第11个黑色梯形的面积S11=84.
分析 由等腰直角三角形的性质和梯形面积公式分别求出S1,S2,S3,…,得出规律,即可求出S11.
解答 解:根据题意得:
S1=$\frac{1}{2}$(1+3)×2=4,
S2=$\frac{1}{2}$(5+7)×2=12,
S3=$\frac{1}{2}$(9+11)×2=20,…,
第n个梯形面积为:Sn=4+8(n-1)=8n-4,
∴S11=8×11-4=84.
故答案为:84.
点评 本题考查了直角梯形的性质、等腰直角三角形的性质以及梯形面积的计算;由梯形的面积得出规律是解决问题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
9.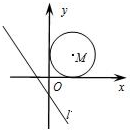 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )| A. | 2.5 | B. | 5-2$\sqrt{2}$ | C. | 2.5或10 | D. | 5-2$\sqrt{2}$或5+2$\sqrt{2}$ |
7.下列运算正确的是( )
| A. | 2x2÷x2=2x | B. | (-$\frac{1}{2}$a2b)3=-$\frac{1}{6}$a6b3 | C. | 3x2+2x2=5x2 | D. | (x-3)2=x2-9 |
4.下列说法中错误的是( )
| A. | 一个锐角的补角一定是钝角 | |
| B. | 同角或等角的余角相等 | |
| C. | 两点间的距离是连结这两点的线段的长度 | |
| D. | 过直线l上的一点有且只有一条直线垂直于l |
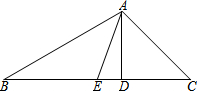 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,∠B=30°,求tan∠DAE的值.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,∠B=30°,求tan∠DAE的值.