题目内容
19.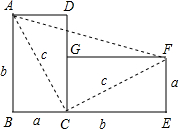 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.
分析 根据S梯形ABEF=S△ABC+S△CEF+S△ACF,利用三角形以及梯形的面积公式即可证明.
解答 证明:该定理的名称是勾股定理,
故答案为:勾股定理;
∵S梯形ABEF=$\frac{1}{2}$(EF+AB)•BE=$\frac{1}{2}$(a+b)•(a+b)=$\frac{1}{2}$(a+b)2,
∵Rt△CDA≌Rt△CGF,
∴∠ACD=∠CFG,
∵∠CFG+∠GCF=90°,
∴∠ACD+∠GCF=90°,
即∠ACF=90°,
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴S梯形ABEF=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2,
∴$\frac{1}{2}$(a+b)2=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
点评 本题考查了用数形结合来证明勾股定理,证明勾股定理常用的方法是利用面积证明,本题锻炼了同学们的数形结合的思想方法.

练习册系列答案
相关题目
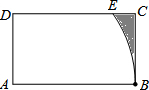 如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则阴影部分的面积是8-2$\sqrt{3}$-$\frac{4π}{3}$(结果保留π).
如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则阴影部分的面积是8-2$\sqrt{3}$-$\frac{4π}{3}$(结果保留π). 在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8.
在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8. 如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.
如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.