题目内容
10.若关于x的方程$\frac{2}{x-2}$+$\frac{mx+1}{{x}^{2}-4}$=0有增根x=-2,则m的值为$\frac{1}{2}$.分析 将分式方程化为整式方程后将x=2代入即可求出答案.
解答 解:2(x+2)+mx+1=0
由题意可知:x=-2是2(x+2)+mx+1=0的根,
∴-2×4+2m+1=0
∴m=$\frac{1}{2}$
故答案为:$\frac{1}{2}$
点评 本题考查分式方程,解题的关键是熟练熟练运用分式方程的解法,本题属于基础题型.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
18.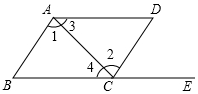 如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )
如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )
 如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )
如图,点E在BC的延长线上,由下列条件能得到AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠B=∠DCE | D. | ∠D+∠DAB=180° |
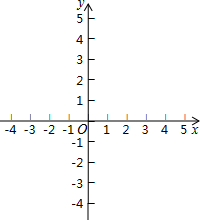 已知点O(0,0),B(1,2).
已知点O(0,0),B(1,2).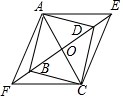 如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.
如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF. 如图,菱形ABCD的边长为6,BD=6,E、F分别是边AD、CD上的两个动点,且满足AE+CF=6.
如图,菱形ABCD的边长为6,BD=6,E、F分别是边AD、CD上的两个动点,且满足AE+CF=6.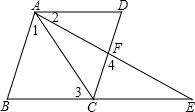 如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.
如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.