题目内容
13.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -11 | … |
分析 利用表格的对应值可判断抛物线的顶点坐标为(0,1),开口向下,于是得到抛物线与x轴有两个交点,然后利用△=b2-4ac决定抛物线与x轴的交点个数可b2-4ac的符号.
解答 解:由表格数据得抛物线过点(-1,-2),(0,1),(1,-2),
所以抛物线的顶点坐标为(0,1),开口向下,
所以抛物线与x轴有两个交点,
所以△=b2-4ac>0.
故答案为>.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
1.若一个多边形的内角和等于900°,则这个多边形的边数是( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
 如图,是矗立在高速公路地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌CD的高度.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
如图,是矗立在高速公路地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌CD的高度.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73). 如图,OM与OB是两坐标轴夹角的三等分线,点E是OM上一点,EC⊥x轴于C点,ED⊥OB于D点.(1)求证:∠ECD=∠EDC;
如图,OM与OB是两坐标轴夹角的三等分线,点E是OM上一点,EC⊥x轴于C点,ED⊥OB于D点.(1)求证:∠ECD=∠EDC;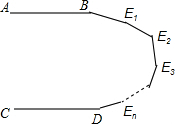 如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=180n度(用含n的代数式表示)
如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=180n度(用含n的代数式表示)