题目内容
3. 如图,是矗立在高速公路地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌CD的高度.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
如图,是矗立在高速公路地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌CD的高度.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
分析 首先根据等腰直角三角形的性质可得DM=AM=4m,再根据勾股定理可得MC2+MB2=(2MC)2,代入数可得答案.
解答 解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4$\sqrt{3}$,
则DC=4$\sqrt{3}$-4≈2.92(米).
点评 此题主要考查了勾股定理得应用,关键是掌握直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
13.在下列各点中,不在函数y=$\frac{6}{x}$的图象上的点是( )
| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (-1,-6) |
14.下列运算正确的是( )
| A. | -$\sqrt{(-13)^{2}}$=13 | B. | $\sqrt{(-6)^{2}}$=-6 | C. | -$\sqrt{25}$=-5 | D. | $\sqrt{9}$=±3 |
8.一个不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同,从袋子中随机地摸出2个球,这2个球都是白球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
12.计算:(-32)÷(-8)的结果是( )
| A. | -32 | B. | -8 | C. | -4 | D. | 4 |
13.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
由表格的数据判断b2-4ac>0(填>,<或=)
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -11 | … |
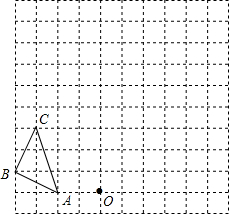 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;