题目内容
18.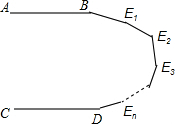 如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=180n度(用含n的代数式表示)
如图,直线AB∥CD,E1,E2…En是两直线间的n个点,那么∠B+∠E1+∠E2+…+∠En+∠D=180n度(用含n的代数式表示)
分析 根据平行线的性质得出规律进行解答即可.
解答 解: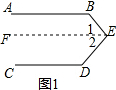 如图1,过E作EF∥AB,则EF∥CD,
如图1,过E作EF∥AB,则EF∥CD,
∴∠B+∠1=180°①,
∠D+∠1=180°②,
①+②得∠B+∠1+∠D+∠2=360°,
即∠B+∠D+∠E=360°,
分别过E1,E2作E1F∥AB,E2G∥AB,则E1F∥E2G∥CD,如图2,
∴∠1+∠B=∠2+∠3=∠4+∠D=180°,
∴∠1+∠B+∠2+∠3+∠4+∠D=540°=3×180°,
所以可得:拐点的个数n与角的和之间的关系是(n+1)•180°,
∴∠B+∠E1+∠E2+∠E3+…+∠En-1+∠D=(n+1-1)•180°=n180°,
故答案为:180n
点评 本题考查的是平行线的性质,根据题意作出辅助线,利用平行线的性质求解是解答此题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
8.一个不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同,从袋子中随机地摸出2个球,这2个球都是白球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
13.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
由表格的数据判断b2-4ac>0(填>,<或=)
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -11 | … |
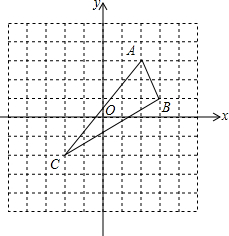 如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出E、F的坐标.
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出E、F的坐标. 如图,EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.