题目内容
8. 如图,OM与OB是两坐标轴夹角的三等分线,点E是OM上一点,EC⊥x轴于C点,ED⊥OB于D点.(1)求证:∠ECD=∠EDC;
如图,OM与OB是两坐标轴夹角的三等分线,点E是OM上一点,EC⊥x轴于C点,ED⊥OB于D点.(1)求证:∠ECD=∠EDC;(2)求证:OC=OD;
(3)试判断OE与线段CD的位置关系,并说明理由.
分析 (1)要证∠ECD=∠EDC,只需证DE=EC,由角平分线的性质可知:DE=EC是成立的;
(2)证明Rt△ODE≌Rt△OCE全等即可;
(3)由OD=OC,ED=EC可知OE垂直平分CD.
解答 (1)证明:∵EC⊥x轴于C点,ED⊥OB于D点,OE平分∠DOC,
∴DE=EC,
∴∠ECD=∠EDC;
(2)解:在Rt△ODE和Rt△OCE中
$\left\{\begin{array}{l}{DE=EC}\\{OE=OE}\end{array}\right.$
∴Rt△ODE≌Rt△OCE(HL),
∴OC=OD;
(3)OE垂直平分CD.理由如下:
证明:∵OE为∠COD的平分线,且OC=OD
∴OE垂直平分CD.
点评 本题主要考查了角平分线的性质、全等三角表的判定与性质,线段垂直平分线的判定,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.正方形的对称轴有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
13.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
由表格的数据判断b2-4ac>0(填>,<或=)
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -11 | … |
20. 如图,边长为3的正△ABC内接于⊙O,点P是$\widehat{AB}$上的动点,则PA+PB的最大值是( )
如图,边长为3的正△ABC内接于⊙O,点P是$\widehat{AB}$上的动点,则PA+PB的最大值是( )
 如图,边长为3的正△ABC内接于⊙O,点P是$\widehat{AB}$上的动点,则PA+PB的最大值是( )
如图,边长为3的正△ABC内接于⊙O,点P是$\widehat{AB}$上的动点,则PA+PB的最大值是( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{3}$ |
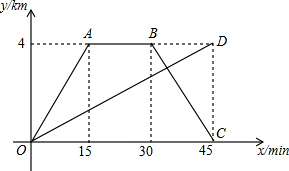 甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)
甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)