Question

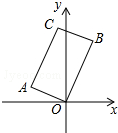如图，在矩形AOBC中，点A的坐标是（-2，1），点C的纵坐标是4，则B、C两点的坐标分别是

 

．

Answer 1

考点：矩形的性质,坐标与图形性质

专题：

分析：首先过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，过点C作CF∥y轴，过点A作AF∥x轴，交点为F，易得△CAF≌△BOE，△AOD∽△OBE，然后由相似三角形的对应边成比例，求得答案．

解答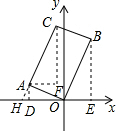：解：过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，过点C作CF∥y轴，过点A作AF∥x轴，交点为F，延长CA交x轴于点H，
∵四边形AOBC是矩形，
∴AC∥OB，AC=OB，
∴∠CAF=∠BOE=∠CHO，
在△ACF和△OBE中，

∠F=∠BEO=90° ∠CAF=∠BOE AC=OB

，
∴△CAF≌△BOE（AAS），
∴BE=CF=4-1=3，
∵∠AOD+∠BOE=∠BOE+∠OBE=90°，
∴∠AOD=∠OBE，
∵∠ADO=∠OEB=90°，
∴△AOD∽△OBE，
∴

AD

OE

=

OD

BE

，
即

1

OE

=

2

3

，
∴OE=

3

2

，
即点B（

3

2

，3），
∴AF=OE=

3

2

，
∴点C的横坐标为：-（2-

3

2

）=-

1

2

，
∴点C（-

1

2

，4）．
故答案是：（

3

2

，3）、（-

1

2

，4）．

点评：此题考查了矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．