题目内容
7．
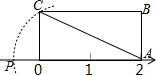如图，长方形OABC放在数轴上，OA=2，OC=1，以A为圆心，AC长为半径画弧交数轴于P点，则P点表示的数为（ ）| A． | 2-$\sqrt{5}$ | B． | -$\sqrt{5}$ | C． | $\sqrt{5}-2$ | D． | $\sqrt{5}-3$ |
分析 利用勾股定理列式求出AC，然后根据数轴写出点P所表示的数即可．
解答 解：∵长方形OABC的长OA为2，宽OC为1，
∴由勾股定理得，AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴AP=$\sqrt{5}$，
∵点A表示的数是2，
∴点P表示的数是2-$\sqrt{5}$．
故选A．
点评 本题考查了勾股定理，实数与数轴，主要是无理数在数轴上的表示，熟记定理是解题的关键．
练习册系列答案
相关题目
甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0.5h，休息前后速度相同，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．
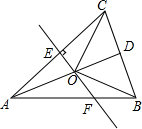如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等的三角形的对数是4．
数轴上A、B（A左B右）所对应的数为a，b，|a+5|+（b-10）2=0，C为数轴上一动点且对应的数为c，O为原点．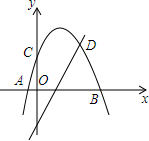
如图，抛物线y=ax2+bx+c关于直线x=1对称，与坐标轴交于A，B，C三点，且AB=4，点D（2，$\frac{3}{2}$）在抛物线上，直线l是一次函数y=kx-2（k≠0）的图象，点O是坐标原点．