题目内容
18.若直线y1上的每个点都可以表示为$(\frac{1}{2}m-2,m)$,且直线y1和y轴交点为点A,和直线y=-2x交点为点B,若点O为坐标原点,则△AOB的面积为2.分析 由于点A在y轴上,因此$\frac{1}{2}$m-2=0,从而可求出m,就可得到点A的坐标,由于点B在直线y=-2x上,把$(\frac{1}{2}m-2,m)$代入y=-2x,从而可求出m,就可得到点B的坐标,就可求出△AOB的面积.
解答 解:当$\frac{1}{2}$m-2=0时,m=4,则点A的坐标为(0,4);
由m=-2($\frac{1}{2}$m-2)得m=2,则点B的坐标为(-1,2);
∴S△AOB=$\frac{1}{2}$×4×|-1|=2.
故答案为2.
点评 本题主要考查直线上点的坐标特征,若点(m,n)在直线y=kx+b上,则有n=km+b.另外,点(x,y)到x轴的距离为|y|,到y轴的距离为|x|.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.若函数y=$(3-m){x^{{m^2}-8}}$是正比例函数,则常数m的值是( )
| A. | -$\sqrt{7}$ | B. | ±$\sqrt{7}$ | C. | ±3 | D. | -3 |
7.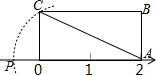 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
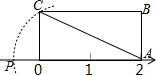 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )| A. | 2-$\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}-2$ | D. | $\sqrt{5}-3$ |
 如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.
如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.