题目内容
19. 数轴上A、B(A左B右)所对应的数为a,b,|a+5|+(b-10)2=0,C为数轴上一动点且对应的数为c,O为原点.
数轴上A、B(A左B右)所对应的数为a,b,|a+5|+(b-10)2=0,C为数轴上一动点且对应的数为c,O为原点.(1)若BC=2,求c的值;
(2)是否存在一点C使得CB=2CA?若存在,求出对应的数为c;若不存在,请说明理由;
(3)是否存在一点C使得CA+CB=21?若存在,求出对应的数c;若不存在,请说明理由.
分析 利用非负数的性质求出a与b的值;
(1)由BC=2求出c的值即可;
(2)存在两点C使得CB=2CA,根据C位置求出c的值即可;
(3)存在两点C使得CA+CB=21,根据C位置求出c的值即可.
解答 解:由|a+5|+(b-10)2=0,得到a=-5,b=10,
(1)若BC=2,即|10-c|=2,
解得:c=8或12;
(2)存在两个点C,使CB=2CA,
当C在A的左侧时,由CB=2CA,得到A为BC的中点,即c=-20;
当C在线段AB上时,由CB=2CA,得到CB=10,CA=5,此时c=0;
(3)存在两个点C,使CA+CB=21,
根据题意得:|c+5|+|c-10|=21,
当C在A的左边时,可得-c-5+10-c=21,解得:c=-2;
当C在B的右边时,可得c-10+c+5=21,解得:c=13.
点评 此题考查了一元一次方程的应用,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.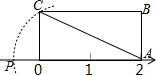 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
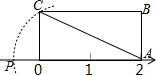 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )| A. | 2-$\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}-2$ | D. | $\sqrt{5}-3$ |
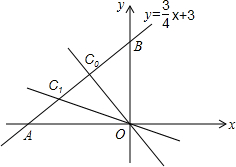 一次函数y=$\frac{3}{4}$x+m的图象过点(4,6),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动.
一次函数y=$\frac{3}{4}$x+m的图象过点(4,6),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动.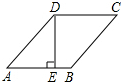 如图,在菱形ABCD中.DE⊥AB于E,DE=2,∠C=45°,则BE长是2$\sqrt{2}$-2.
如图,在菱形ABCD中.DE⊥AB于E,DE=2,∠C=45°,则BE长是2$\sqrt{2}$-2.