题目内容
(1)已知:如图1,直线AC∥BD,求证:∠APB=∠PAC+∠PBD;
(2)如图2,如果点P在AC与BD之内,线段AB的左侧,其它条件不变,那么会有什么结果?并加以证明;
(3)如图3,如果点P在AC与BD之外,其他条件不变,你发现的结果是 (只写结果,不要证明).

(2)如图2,如果点P在AC与BD之内,线段AB的左侧,其它条件不变,那么会有什么结果?并加以证明;
(3)如图3,如果点P在AC与BD之外,其他条件不变,你发现的结果是

考点:平行线的性质
专题:
分析:(1)过P作PM∥AC,根据平行线的性质得出∠1=∠PAC,∠2=∠PBD,即可得出答案;
(2)过P作PM∥AC,根据平行线的性质得出∠1+∠PAC=180°,∠2+∠PBD=180°,相加即可;
(3)过P作PM∥AC,根据平行线的性质得出∠MPA=∠PAC,∠MPB=∠PBD,即可得出答案.
(2)过P作PM∥AC,根据平行线的性质得出∠1+∠PAC=180°,∠2+∠PBD=180°,相加即可;
(3)过P作PM∥AC,根据平行线的性质得出∠MPA=∠PAC,∠MPB=∠PBD,即可得出答案.
解答:(1)证明: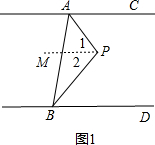
如图1,过P作PM∥AC,
∵AC∥BD,
∴AC∥BD∥PM,
∴∠1=∠PAC,∠2=∠PBD,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)∠APB+∠PBD+∠PAC=360°,
证明:如图2,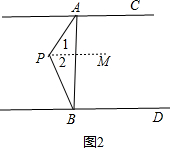
过P作PM∥AC,
∵AC∥BD,
∴AC∥BD∥PM,
∴∠1+∠PAC=180°,∠2+∠PBD=180°,
∴∠1+∠PAC+∠2+∠PBD=360°,
即∠APB+∠PBD+∠PAC=360°;
(3)∠APB=∠PBD-∠PAC,
证明:过P作PM∥AC,如图3,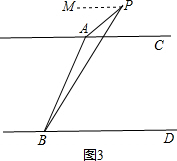
∵AC∥BD,
∴AC∥BD∥PM,
∴∠MPA=∠PAC,∠MPB=∠PBD,
∴∠APB=∠MPB-∠MPA=∠PBD-∠PAC,
故答案为:∠APB=∠PBD-∠PAC.

如图1,过P作PM∥AC,
∵AC∥BD,
∴AC∥BD∥PM,
∴∠1=∠PAC,∠2=∠PBD,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)∠APB+∠PBD+∠PAC=360°,
证明:如图2,

过P作PM∥AC,
∵AC∥BD,
∴AC∥BD∥PM,
∴∠1+∠PAC=180°,∠2+∠PBD=180°,
∴∠1+∠PAC+∠2+∠PBD=360°,
即∠APB+∠PBD+∠PAC=360°;
(3)∠APB=∠PBD-∠PAC,
证明:过P作PM∥AC,如图3,

∵AC∥BD,
∴AC∥BD∥PM,
∴∠MPA=∠PAC,∠MPB=∠PBD,
∴∠APB=∠MPB-∠MPA=∠PBD-∠PAC,
故答案为:∠APB=∠PBD-∠PAC.
点评:本题考查了平行线的性质的应用,解此题的关键是能正确作辅助线,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.

练习册系列答案
相关题目
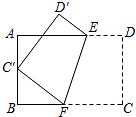 如图所示,将矩形ABCD沿直线EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
如图所示,将矩形ABCD沿直线EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )| A、4 | ||
B、3
| ||
| C、4.5 | ||
D、2
|


 如图,在平面内有A、B、C三点.
如图,在平面内有A、B、C三点.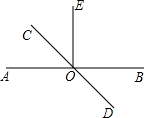 如图,直线AB和CD相交于点O,OE⊥AB,∠AOD=125°,则∠COE的度数是
如图,直线AB和CD相交于点O,OE⊥AB,∠AOD=125°,则∠COE的度数是 青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)
青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)