题目内容
5.如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长4πcm(结果保留π).
分析 观察顶点O经过的路线,可以看出顶点O经过的路线分为三段,分别求出三段的长,再求出它的总和即是顶点O经过的路线总长.
解答 解:顶点O经过的路线可以分为三段,
第一段:当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°.
此时点O经过了以O为圆心,以3为半径的圆的周长的$\frac{1}{4}$,即经过了$\frac{1}{4}$×2π×3=$\frac{3}{2}π$;
第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,
所以O与转动点的连线始终⊥直线l,
所以O点在水平运动,此时O点经过的路线长=BA’=AB的弧长=$\frac{60×π×3}{180}$=π;
第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°,
此时点O经过了以O为圆心,以3为半径的圆的周长的$\frac{1}{4}$,即经过了$\frac{1}{4}$×2π×3=$\frac{3}{2}π$;
所以,O点经过的路线总长S=$\frac{3}{2}π$+π+$\frac{3}{2}π$=4π.
故答案为4π.
点评 本题考查了圆的周长公式、弧长公式.能够看懂图,知道点O经过的三段是解决本题的关键.弧长公式=$\frac{nπr}{180}$.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
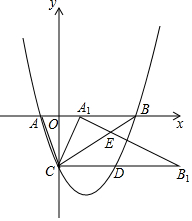 如图,已知抛物线与y轴交于点C(0,-3),与x轴交于点A(-1,0)B(4,0),将△ABC绕点C顺时针旋转α得△A1B1C(点A,B的对应点分别为点A1,B1),CB1交抛物线于点D,射线A1B1与射线BC交于点E.
如图,已知抛物线与y轴交于点C(0,-3),与x轴交于点A(-1,0)B(4,0),将△ABC绕点C顺时针旋转α得△A1B1C(点A,B的对应点分别为点A1,B1),CB1交抛物线于点D,射线A1B1与射线BC交于点E.
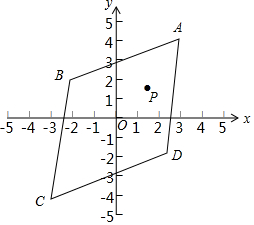 如图,P(x0,y0)为平行四边形ABCD内任意一点,若将平行四边形作平移变换,使AD落在BC的位置上,则移动后点P所在位置的坐标为(x0-5,y0-2).
如图,P(x0,y0)为平行四边形ABCD内任意一点,若将平行四边形作平移变换,使AD落在BC的位置上,则移动后点P所在位置的坐标为(x0-5,y0-2). 如图所示,在△ABC中,∠A=40°,BC=3,分别以点B,C为圆心,BC长为半径在BC右侧画弧,两弧交于点D,与AB,AC延长线分别交于点E,F,则$\widehat{DE}$和$\widehat{DF}$的长度和为$\frac{5π}{3}$.
如图所示,在△ABC中,∠A=40°,BC=3,分别以点B,C为圆心,BC长为半径在BC右侧画弧,两弧交于点D,与AB,AC延长线分别交于点E,F,则$\widehat{DE}$和$\widehat{DF}$的长度和为$\frac{5π}{3}$.