题目内容
13.先化简,再求值:$\frac{{b}^{2}-{a}^{2}}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=$\sqrt{3}+1$,b=$\sqrt{3}-1$.分析 先根据分式的混合运算顺序和法则化简原式,再代入求值即可得.
解答 解:原式=$\frac{(b-a)(b+a)}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{(b+a)(b-a)}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{b+a}{b-a}$,
当a=$\sqrt{3}+1$,b=$\sqrt{3}-1$时,
原式=$\frac{\sqrt{3}+1+\sqrt{3}-1}{\sqrt{3}-1-\sqrt{3}-1}$=$\frac{2\sqrt{3}}{-2}$=-$\sqrt{3}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
相关题目
4.一个寻宝游戏的通道平面图如图1所示(正方形ABCD是⊙O的内接四边形),图中的所有线段和弧线都是通道.为了记录寻宝者的行进路线,相关人员在点O处放置了一台定位仪器.设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x之间的函数关系的图象如图2所示,则寻宝者的行进路线可能为…( )
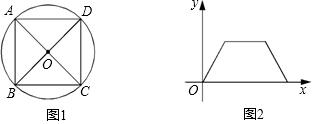

| A. | 线段OA→劣弧AD→线段DO | B. | 劣弧AD→线段DO→线段OC | ||
| C. | 劣弧AD→劣弧DC→线段CO | D. | 线段OB→劣弧BC→劣弧CD |
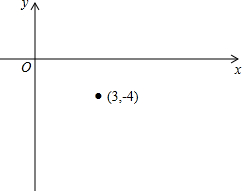 已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).
已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).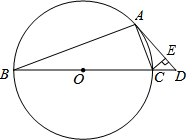 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,作∠CAD=∠B,且点E在BC的延长线上,CE⊥AD于点E,
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,作∠CAD=∠B,且点E在BC的延长线上,CE⊥AD于点E,
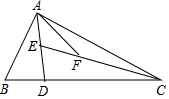 如图,BC=5BD,E是AD的中点,F是EC的三等分点,已知△AEF的面积是4平方厘米,则△ABD的面积多少平方厘米?
如图,BC=5BD,E是AD的中点,F是EC的三等分点,已知△AEF的面积是4平方厘米,则△ABD的面积多少平方厘米?