题目内容
4.已知:将一副三角板(Rt△ABC和Rt△DEF)如图①摆放,点E,A,D,B在一条直线上,且D是AB的中点.将Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE,AC相交于点M,直线DF,BC相交于点N,分别过点M,N作直线AB的垂线,垂足为G,H.(1)当α=30°时(如图②),求证:AG=DH;
(2)当α=60°时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由;
(3)当0°<α<90°(如图④)时,求证:AG•HB=GD•DH.

分析 (1)由题意确定出∠A=∠MDA,利用等角对等边得到MA=MD,利用三线合一得到AG=GD,再由MG垂直于AD,得到AG垂直于AD,进而确定出三角形CDB为等边三角形,根据CH垂直于BD,利用三线合一得到H为BD中点,再由D为AB中点,等量代换即可得证;
(2)AG=DH,理由为:根据题意,利用ASA得到三角形AMD与三角形DNB全等,利用全等三角形对应边相等得到AM=DN,再由两直线平行同位角相等,以及一对直角相等,利用AAS得到三角形AMG与三角形DNH全等,利用全等三角形对应边相等即可得证;
(3)利用两对角相等的三角形相似得到三角形AMG与三角形NHB相似,由相似得比例,再利用两对角相等的三角形相似得到三角形MGD与三角形DHN相似,由相似得比例,等量代换即可得证.
解答 (1)证明:∵∠A=∠MDA=α=30°,
∴MA=MD,
又∵MG⊥AD,
∴AG=$\frac{1}{2}$AD,
∵∠FDB=90°-α=90°-30°=60°,∠B=60°,
∴△CDB是等边三角形,
又∵CH⊥BD,
∴DH=$\frac{1}{2}$BD,
∵D为AD的中点,
∴AD=BD,
∴AG=DH;
(2)解:AG=DH,理由为:
在△AMD和△DNB中,
$\left\{\begin{array}{l}{∠A=∠NDB}\\{AD=BD}\\{∠B=∠MDA=60°}\end{array}\right.$,
∴△AMD≌△DNB(ASA),
∴AM=DN,
又∵∠A=∠NDH=90°-α=90°-60°=30°,∠AGM=∠DHN=90°,
∴△AGM≌△DHN(AAS),
∴AG=DH;
(3)证明:在Rt△AGM中,∠A=30°,
∴∠AMG=90°-30°=60°=∠B,
又∵∠AGM=∠NHB=90°,
∴△AGM∽△NHB,
∴$\frac{MG}{AG}$=$\frac{HB}{NH}$,
∴MG•NH=AG•HB,
∵∠GMD+∠GDM=90°,∠HDN+∠GDM=90°,
∴∠GMD=∠HDN,
又∵∠MGD=∠DHN=90°,
∴△MGD∽△DHN,
∴$\frac{GD}{MG}$=$\frac{HN}{DH}$,
∴MG•NH=GD•DH,
∴AG•HB=GD•GH.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形的性质,以及等边三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

| A. | 3a2-a2=3 | B. | a2•a4=a8 | C. | a8÷a2=a5 | D. | (a3)2=a6 |
| A. | x3•x2=x4 | B. | x(x-2)=-2x+x2 | C. | (x+y)(x-y)=x2+y2 | D. | 3x3y2÷xy2=3x4 |
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米)部分 | 0.4 |
| 超过30平方米部分 | 0.9 |
(1)请求出y关于x的函数关系式;
(2)若某3人之家欲购买120平方米的商品房,求其应缴纳的房款.
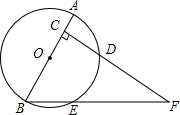 如图,己知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
如图,己知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.