题目内容
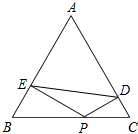 如图,已知P是等边△ABC的BC边上任意一点,过P点分别作AB、AC的垂线PE、PD,垂足为E、D.问:△AED的周长与四边形EBCD的周长之间的关系?
如图,已知P是等边△ABC的BC边上任意一点,过P点分别作AB、AC的垂线PE、PD,垂足为E、D.问:△AED的周长与四边形EBCD的周长之间的关系?考点:等边三角形的性质,含30度角的直角三角形
专题:
分析:△AED的周长与四边形EBCD的周长相等.由于DE是△AED与四边形EBCD的公共边,所以只需证明AD+AE=BE+BC+CD.
解答:解:△AED的周长与四边形EBCD的周长相等.理由如下:
在等边△ABC中,∠B=∠C=60°,
 ∵PE⊥AB于E,PD⊥AC于D,
∵PE⊥AB于E,PD⊥AC于D,
∴∠BPE=∠CPD=30°.
不妨设等边△ABC的边长为1,BE=x,CD=y,那么BP=2x,PC=2y,
∵2x+2y=1,
∴x+y=
,
∵AE=1-x,AD=1-y,
∴AE+AD=2-(x+y)=
,
又∵BE+CD+BC=(x+y)+1=
,
∴AD+AE=BE+BC+CD,
∴AD+AE+DE=BE+BC+CD+DE,
即△AED的周长与四边形EBCD的周长相等.
在等边△ABC中,∠B=∠C=60°,
 ∵PE⊥AB于E,PD⊥AC于D,
∵PE⊥AB于E,PD⊥AC于D,∴∠BPE=∠CPD=30°.
不妨设等边△ABC的边长为1,BE=x,CD=y,那么BP=2x,PC=2y,
∵2x+2y=1,
∴x+y=
| 1 |
| 2 |
∵AE=1-x,AD=1-y,
∴AE+AD=2-(x+y)=
| 3 |
| 2 |
又∵BE+CD+BC=(x+y)+1=
| 3 |
| 2 |
∴AD+AE=BE+BC+CD,
∴AD+AE+DE=BE+BC+CD+DE,
即△AED的周长与四边形EBCD的周长相等.
点评:本题考查了等边三角形的性质,含30度角的直角三角形的性质,三角形、四边形的周长,难度适中.设出辅助未知数,运用整体思想是解题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、任何数的平方根有两个 |
| B、只有正数才有平方根 |
| C、一个正数的平方根的平方仍是这个数 |
| D、a2的平方根是a |