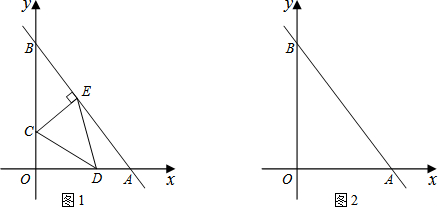题目内容
 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2-7x+12=0的两个根(OA>OB).
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2-7x+12=0的两个根(OA>OB).(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
考点:一次函数综合题,全等三角形的判定与性质,等腰直角三角形,正方形的性质
专题:压轴题
分析:(1)解一元二次方程求出OA、OB的长度,过点D作DE⊥y于点E,根据正方形的性质可得AD=AB,∠DAB=90°,然后求出∠ABO=∠DAE,然后利用“角角边”证明△DAE和△ABO全等,根据全等三角形对应边相等可得DE=OA,AE=OB,再求出OE,然后写出点D的坐标即可;
(2)过点C作CM⊥x轴于点M,同理求出点C的坐标,设直线BC的解析式为y=kx+b(k≠0,k、b为常数),然后利用待定系数法求一次函数解析式解答;
(3)根据正方形的性质,点P与点B重合时,△PCD为等腰三角形;点P为点B关于点C的对称点时,△PCD为等腰三角形,然后求解即可.
(2)过点C作CM⊥x轴于点M,同理求出点C的坐标,设直线BC的解析式为y=kx+b(k≠0,k、b为常数),然后利用待定系数法求一次函数解析式解答;
(3)根据正方形的性质,点P与点B重合时,△PCD为等腰三角形;点P为点B关于点C的对称点时,△PCD为等腰三角形,然后求解即可.
解答:解:(1)x2-7x+12=0,
解得x1=3,x2=4,
∵OA>OB,
∴OA=4,OB=3,
过D作DE⊥y于点E,
∵正方形ABCD,
∴AD=AB,∠DAB=90°,
∠DAE+∠OAB=90°,
∠ABO+∠OAB=90°,
∴∠ABO=∠DAE,
∵DE⊥AE,
∴∠AED=90°=∠AOB,
在△DAE和△ABO中,
,
∴△DAE≌△ABO(AAS),
∴DE=OA=4,AE=OB=3,
∴OE=7,
∴D(4,7);
(2)过点C作CM⊥x轴于点M,
同上可证得△BCM≌△ABO,
∴CM=OB=3,BM=OA=4,
∴OM=7,
∴C(7,3),
设直线BC的解析式为y=kx+b(k≠0,k、b为常数),
代入B(3,0),C(7,3)得,
,
解得
,
∴y=
x-
;
(3)存在,如图,
点P与点B重合时,P1(3,0),
点P与点B关于点C对称时,P2(11,6).
解得x1=3,x2=4,
∵OA>OB,
∴OA=4,OB=3,
过D作DE⊥y于点E,
∵正方形ABCD,
∴AD=AB,∠DAB=90°,

∠DAE+∠OAB=90°,
∠ABO+∠OAB=90°,
∴∠ABO=∠DAE,
∵DE⊥AE,
∴∠AED=90°=∠AOB,
在△DAE和△ABO中,
|
∴△DAE≌△ABO(AAS),
∴DE=OA=4,AE=OB=3,
∴OE=7,
∴D(4,7);
(2)过点C作CM⊥x轴于点M,
同上可证得△BCM≌△ABO,
∴CM=OB=3,BM=OA=4,
∴OM=7,
∴C(7,3),
设直线BC的解析式为y=kx+b(k≠0,k、b为常数),

代入B(3,0),C(7,3)得,
|
解得
|
∴y=
| 3 |
| 4 |
| 9 |
| 4 |
(3)存在,如图,
点P与点B重合时,P1(3,0),
点P与点B关于点C对称时,P2(11,6).
点评:本题是一次函数综合题型,主要利用了解一元二次方程,正方形的性质,全等三角形的判定与性质,待定系数法求一次函数解析式,等腰直角三角形的判定与性质,(1)作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
把不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为
如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为