题目内容
如图,在平面直角坐标系中,直线y=-
x+b与x轴交于点A(6,0),与y轴交于点B.
(1)填空:b= ;
(2)点C在线段OB上,其坐标为(0,m),过点C作CE⊥AB于点E,点D为线段OA上的一个动点,连接CD、DE.
①当m=3,且DE∥y轴时,求点D的坐标;
②在点D运动的过程中,是否存在以CE为直径的圆恰好与x轴相切于点D?若存在,求出m的值;若不存在,请说明理由.
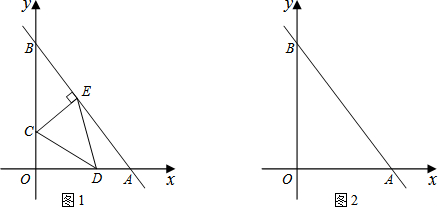
| 4 |
| 3 |
(1)填空:b=
(2)点C在线段OB上,其坐标为(0,m),过点C作CE⊥AB于点E,点D为线段OA上的一个动点,连接CD、DE.
①当m=3,且DE∥y轴时,求点D的坐标;
②在点D运动的过程中,是否存在以CE为直径的圆恰好与x轴相切于点D?若存在,求出m的值;若不存在,请说明理由.
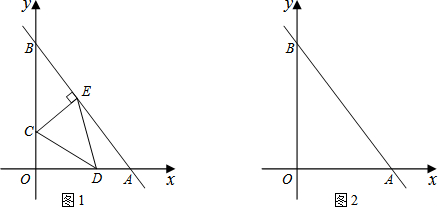
考点:一次函数综合题
专题:
分析:(1)直接把点A(6,0)代入直线y=-
x+b,求出b的值即可;
(2)①先求出点B的坐标,根据勾股定理求出AB的长,再由相似三角形的判定定理得出△BCE∽△BAO,得出BE及AE的长,再根据△EDA∽△BOA得出OD的长,进而得出结论;
②取CE的中点P,过P作PG⊥y轴于点G.由△BCE∽△BAO可得CE=
-
m,先求出∠GCP=∠BAO,cos∠GCP=cos∠BAO,CG=CP•cos∠GCP,OG=OC+CG,当OG=CP时,⊙P恰好与x轴相切于点D,由OG=CP得出关于m的一元一次方程,求出m的值即可.
| 4 |
| 3 |
(2)①先求出点B的坐标,根据勾股定理求出AB的长,再由相似三角形的判定定理得出△BCE∽△BAO,得出BE及AE的长,再根据△EDA∽△BOA得出OD的长,进而得出结论;
②取CE的中点P,过P作PG⊥y轴于点G.由△BCE∽△BAO可得CE=
| 24 |
| 5 |
| 3 |
| 5 |
解答: 解:(1)∵直线y=-
解:(1)∵直线y=-
x+b与x轴交于点A(6,0),
∴(-
)×6+b=0,解得b=8.
故答案为:8;
(2)①由(1)得y=-
x+8当x=0时,y=8,即B(0,8),
∴OA=6,OB=8,
∴AB=
=
=10,
当m=3时,BC=5,
∵∠CEB=∠AOB=90°,
又∵∠OBA=∠EBC,
∴△BCE∽△BAO,
∴
=
,即
=
,
∴BE=4,
∴AE=AB-BE=6.
∴DE∥BO,
∴△EDA∽△BOA,
∴
=
,即
=
,
∴OD=
,
∴点D的坐标为(
,0).
②解法一:取CE的中点P,过P作PG⊥y轴于点G.
由△BCE∽△BAO可得:CE=
-
m,
则CP=
CE=
-
m.
如图2,易证∠GCP=∠BAO,
∴cos∠GCP=cos∠BAO=
,
∴CG=CP•cos∠GCP=
(
-
m)=
-
m.
∴OG=OC+CG=m+
-
m=
m+
.
当OG=CP时,⊙P恰好与x轴相切于点D.
∴
m+
=
-
m,
解得:m=
.
解法二:②取CE的中点P,过E作EH⊥x轴于点H,连结PD.
 由△BCE∽△BAO可得:
由△BCE∽△BAO可得:
CE=
-
m,BE=
-
m,AE=10-BE=
+
m,
如图3,EH⊥x轴 易证∠EHA=∠BOA,∠BAO=∠BAO,
∴△AEH∽△ABO,
∴
=
,
∴EH=
(
+
m)=
+
m,
当 PD⊥x轴时,⊙P恰好与x轴相切于点D.
此时易证点D是OH的中点,即PD是梯形COHE的中位线,
∴CO+EH=2PD=CE,
∴m=
+
m=
-
m,
解得:m=
.
 解:(1)∵直线y=-
解:(1)∵直线y=-| 4 |
| 3 |
∴(-
| 4 |
| 3 |
故答案为:8;
(2)①由(1)得y=-
| 4 |
| 3 |
∴OA=6,OB=8,
∴AB=
| OB2+OA2 |
| 82+62 |
当m=3时,BC=5,
∵∠CEB=∠AOB=90°,
又∵∠OBA=∠EBC,
∴△BCE∽△BAO,
∴
| BE |
| OB |
| BC |
| AB |
| BE |
| 8 |
| 5 |
| 10 |
∴BE=4,
∴AE=AB-BE=6.
∴DE∥BO,
∴△EDA∽△BOA,
∴
| AD |
| OA |
| AE |
| AB |
| 6-OD |
| 6 |
| 6 |
| 10 |
∴OD=
| 12 |
| 5 |
∴点D的坐标为(
| 12 |
| 5 |
②解法一:取CE的中点P,过P作PG⊥y轴于点G.
由△BCE∽△BAO可得:CE=
| 24 |
| 5 |
| 3 |
| 5 |
则CP=
| 1 |
| 2 |
| 12 |
| 5 |
| 3 |
| 10 |
如图2,易证∠GCP=∠BAO,
∴cos∠GCP=cos∠BAO=
| 3 |
| 5 |
∴CG=CP•cos∠GCP=
| 3 |
| 5 |
| 12 |
| 5 |
| 3 |
| 10 |
| 36 |
| 25 |
| 9 |
| 50 |
∴OG=OC+CG=m+
| 36 |
| 25 |
| 9 |
| 50 |
| 41 |
| 50 |
| 36 |
| 25 |
当OG=CP时,⊙P恰好与x轴相切于点D.
∴
| 41 |
| 50 |
| 36 |
| 25 |
| 12 |
| 5 |
| 3 |
| 10 |
解得:m=
| 6 |
| 7 |
解法二:②取CE的中点P,过E作EH⊥x轴于点H,连结PD.
 由△BCE∽△BAO可得:
由△BCE∽△BAO可得:CE=
| 24 |
| 5 |
| 3 |
| 5 |
| 32 |
| 5 |
| 4 |
| 5 |
| 18 |
| 5 |
| 4 |
| 5 |
如图3,EH⊥x轴 易证∠EHA=∠BOA,∠BAO=∠BAO,
∴△AEH∽△ABO,
∴
| EH |
| BO |
| AE |
| AB |
∴EH=
| 4 |
| 5 |
| 18 |
| 5 |
| 4 |
| 5 |
| 72 |
| 25 |
| 16 |
| 25 |
当 PD⊥x轴时,⊙P恰好与x轴相切于点D.
此时易证点D是OH的中点,即PD是梯形COHE的中位线,
∴CO+EH=2PD=CE,
∴m=
| 72 |
| 25 |
| 16 |
| 25 |
| 24 |
| 5 |
| 3 |
| 5 |
解得:m=
| 6 |
| 7 |
点评:本题考查的是一次函数综合题,涉及到相似三角形的判定与性质、勾股定理等知识,难度适中.

练习册系列答案
相关题目
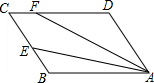 如图,?ABCD中,AB=6,E是BC边的中点,F为CD边上一点,DF=4.8,∠DFA=2∠BAE,则AF的长为( )
如图,?ABCD中,AB=6,E是BC边的中点,F为CD边上一点,DF=4.8,∠DFA=2∠BAE,则AF的长为( )| A、4.8 | B、6 |
| C、7.2 | D、10.8 |
 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2-7x+12=0的两个根(OA>OB).
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2-7x+12=0的两个根(OA>OB).
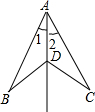 如图所示,已知∠1=∠2,请你添加一个条件,证明:AB=AC.
如图所示,已知∠1=∠2,请你添加一个条件,证明:AB=AC.