题目内容
 如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,
如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,(1)求线段MN的长,
(2)若∠AOB=30°,求OM的长.
考点:轴对称的性质
专题:
分析:(1)根据轴对称的性质可知:EP=EM,PF=FN,所以线段MN的长=△PEF的周长;
(2)连接OM、OP、ON,根据等边三角形的性质得到△MON为等边三角形,从而求得OM的长.
(2)连接OM、OP、ON,根据等边三角形的性质得到△MON为等边三角形,从而求得OM的长.
解答: 解:(1)根据题意,EP=EM,PF=FN,
解:(1)根据题意,EP=EM,PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∴MN=20cm.
(2)连接OM、OP、ON,
∵M、N分别是点P关于直线OA、OB的对称点,
∴∠MOA=∠POA,∠NOB=∠POB,
∵∠AOB=30°,
∴∠MON=2∠AOB=60°,
∴△MON为等边三角形,
∴OM=ON=MN=20cm.
 解:(1)根据题意,EP=EM,PF=FN,
解:(1)根据题意,EP=EM,PF=FN,∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∴MN=20cm.
(2)连接OM、OP、ON,
∵M、N分别是点P关于直线OA、OB的对称点,
∴∠MOA=∠POA,∠NOB=∠POB,
∵∠AOB=30°,
∴∠MON=2∠AOB=60°,
∴△MON为等边三角形,
∴OM=ON=MN=20cm.
点评:此题主要考查了轴对称的性质:对称轴上的任何一点到两个对应点之间的距离相等.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
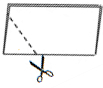 如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )
如图,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )| A、22.5° | B、45° |
| C、60° | D、135° |
下列调查中,适合用全面调查的是( )
| A、某厂生产的电灯使用寿命 |
| B、全国初中生的视力情况 |
| C、七年级某班学生的身高情况 |
| D、某种饮料新产品的合格率 |
某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场共有中、小型汽车50辆,这些车共缴纳停车费230元.4名同学都设未知数为x、y,并根据题意,分别列出以下四个方程组,其中不正确的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
 在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为( )
在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,使点A与点B重合,折痕与AB、AC分别相交于点D和点E(如图),折痕DE的长为( )