题目内容
10.分式$\frac{{x}^{3}}{x}$、$\frac{3a+1}{3a+b}$、$\frac{m+n}{{m}^{2}-{n}^{2}}$、$\frac{2-2x}{2x}$中,最简分式的个数是( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据最简分式的标准是分子、分母中不含有公因式,不能再约分,即可得出答案.
解答 解:∵$\frac{{x}^{3}}{x}$=x2,
$\frac{m+n}{{m}^{2}-{n}^{2}}$=$\frac{m+n}{(m+n)(m-n)}$=m-n,
$\frac{2-2x}{2x}$=$\frac{1-x}{x}$,
∴分式$\frac{{x}^{3}}{x}$、$\frac{3a+1}{3a+b}$、$\frac{m+n}{{m}^{2}-{n}^{2}}$、$\frac{2-2x}{2x}$中,最简分式是$\frac{3a+1}{3a+b}$,共有1个;
故选A.
点评 本题考查了最简分式.分式的化简过程,首先要把分子、分母分解因式,观察分子、分母中有无公因式.

练习册系列答案
相关题目
1.等腰三角形ABC的周长为20cm,AB=8cm,则该等腰三角形的腰长为( )
| A. | 8cm | B. | 6cm | C. | 4cm | D. | 8cm或6cm |
15.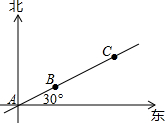 如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )
如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )
 如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )
如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )| A. | C在A的北偏东30°方向的15米处 | B. | A在C的北偏东60°方向的15米处 | ||
| C. | C在B的北偏东60°方向的10米处 | D. | B在A的北偏东30°方向的5米处 |
2.已知(x-3)2+|y-4|=0,则$\frac{x}{y}$的算术平方根是( )
| A. | $±\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $±\frac{{\sqrt{3}}}{4}$ |
19.下列运算正确的是( )
| A. | $\sqrt{18}÷\sqrt{2}=9$ | B. | ${(\frac{1}{3})}^{-2}=\frac{1}{9}$ | C. | (-a2)3=a6 | D. | a6÷($\frac{1}{2}$a2)=2a4 |
20.在平面直角坐标系中,一次函数y=-3x+1的图象所经过的象限是( )
| A. | 二、三、四 | B. | 一、三、四 | C. | 一、二、四 | D. | 一、二、三 |