题目内容
20.若(x2+mx-8)(x2-3x+n)的展开式中不含x2和x3项,则m=3,n=17.分析 利用多项式乘以多项式法则计算得到结果,根据展开式中不含x2和x3项列出关于m与n的方程组,求出方程组的解即可得到m与n的值.
解答 解:原式=x4+(m-3)x3+(n-3m-8)x2+(mn+24)x-8n,
根据展开式中不含x2和x3项得,
$\left\{\begin{array}{l}{m-3=0}\\{n-3m-8=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=3}\\{n=17}\end{array}\right.$.
故答案为:m=3,n=17.
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.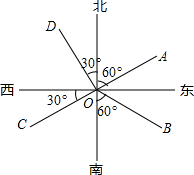 如图所示的四条射线中,表示北偏西30°的是( )
如图所示的四条射线中,表示北偏西30°的是( )
 如图所示的四条射线中,表示北偏西30°的是( )
如图所示的四条射线中,表示北偏西30°的是( )| A. | 射线OA | B. | 射线OB | C. | 射线OC | D. | 射线OD |
8.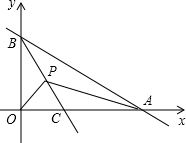 如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
 如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
12.世界第一高峰珠穆朗玛峰,其海拔约8844.43米,是一条近似东西向的弧形山系,近似数8844.43用科学记数法精确到十位,其中正确的是( )
| A. | 88.4×102 | B. | 8.84×103 | C. | 8.80×103 | D. | 8.8×103 |
9.若xn+1×( )=xm-n,则括号内代数式为( )
| A. | Xm+1 | B. | Xm-1 | C. | Xm-2n-1 | D. | Xm-2n+1 |
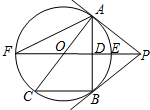 如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,
如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,