题目内容
边长为4的等边三角形绕它的高所在的直线旋转180°，所得的圆锥的表面积为（ ）
| A、12π | ||
B、（4
| ||
C、（8
| ||
| D、8π |
考点：圆锥的计算
专题：
分析：求出圆锥的底面半径，母线长，进而求出圆锥的底面周长，代入圆锥表面积公式，即可求出圆锥的表面积．
解答：解：边长为4的等边三角形绕它的高所在的直线旋转180°得到一个圆锥，轴截面（过旋转轴的截面）是边长为4的等边三角形，
所以圆锥的母线为l=4；底面半径为r=2；
圆锥的底面周长为C=2πr=4π．
所以圆锥的表面积为：
×4π×2+π•22=8π
故选D．
所以圆锥的母线为l=4；底面半径为r=2；
圆锥的底面周长为C=2πr=4π．
所以圆锥的表面积为：
| 1 |
| 2 |
故选D．
点评：本题是基础题，考查圆锥的轴截面知识，圆锥的表面积的求法，实际上这个圆锥又叫等边圆锥，需要同学注意它的边角关系，常考题目．
练习册系列答案
相关题目
如图是一个正方体被截去一角后得到的几何体，它的主视图是（ ）
A、 |
B、 |
C、 |
D、 |
方程2x2+3x-4的根的情况是（ ）
| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、有两个实数根 |
收割机前面的拨禾轮是正五边形，它绕着正五边形的中心在不停地旋转．正五边形绕着它的中心只要旋转多少度就能和原来的图形重合？（ ）
| A、45 | B、60 | C、72 | D、75 |
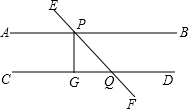如图，AB∥CD，直线EF分别与直线AB和直线CD相交于点P和点Q，PG⊥CD于G，若∠APE=48°，则∠QPG的度数为（ ）| A、42° | B、46° |
| C、32° | D、36° |
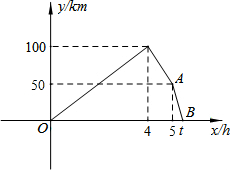甲、乙两车同时从M地出发，以各自的速度匀速向N地行驶．甲车先到达N地，停留1h后按原路以原速匀速返回，直到两车相遇，乙车的速度为50km/h．如图是两车之间的距离y（km）与乙车行驶时间x（h）之间的函数图象．
李明乘车从永康到某景区旅游，同时王红从该景区返回永康．线段OB表示李明离永康的路程S1（km）与时间t（h）的函数关系；线段AC表示王红离永康的路程S2（km）与时间t（h）的函数关系．行驶1小时，李明、王红离永康的路程分别为100km、280km，王红从景区返回永康用了4.5小时．（假设两人所乘的车在同一线路上行驶）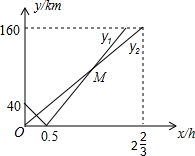
某次海军舰艇演习中，甲、乙两舰艇同时从A、B两个港口出发，均沿直线匀速驶向演习目标地海岛C，两舰艇都到达C岛后演习第一阶段结束．已知B港位于A港、C岛之间，且A、B、C在一条直线上．设甲、乙两舰艇行驶x（h）后，与B港的距离分别为y1和y2（km），y1、y2与x的函数关系如图所示．
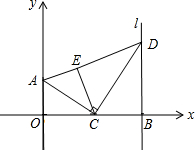如图，点A的坐标是（0，2），点B是x轴正半轴上的点，过点B作直线l垂直于x轴，点C为线段OB上的动点，连接AC，过点C作CD⊥AC交直线l于点D，将△BCD沿CD翻折至△ECD的位置，连接AE，设点B的坐标是（m，0），点C的坐标是（n，0）