题目内容
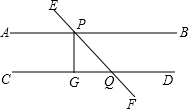如图，AB∥CD，直线EF分别与直线AB和直线CD相交于点P和点Q，PG⊥CD于G，若∠APE=48°，则∠QPG的度数为（ ）| A、42° | B、46° |
| C、32° | D、36° |
考点：平行线的性质
专题：
分析：求出∠PGC=90°，根据平行线的性质求出∠APG=90°，即可求出答案．
解答：解：∵PG⊥CD，
∴∠PGC=90°，
∵AB∥CD，
∴∠APG=180°-∠PGC=90°，
∵∠APE=48°，
∴∠QPG=180°-90°-48°=42°，
故选A．
∴∠PGC=90°，
∵AB∥CD，
∴∠APG=180°-∠PGC=90°，
∵∠APE=48°，
∴∠QPG=180°-90°-48°=42°，
故选A．
点评：本题考查了邻补角，垂直定义，平行线的性质的应用，注意：两直线平行，同旁内角互补．
练习册系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
相关题目
下列等式中：
（1）（a+b）2=a2+b2；
（2）（x-a）（x+b）=x2-（a+b）x-ab；
（3）2a2•2a-1=a；
（4）2a3÷（2a3-a2）=1-2a．
其中不成立的有（ ）
（1）（a+b）2=a2+b2；
（2）（x-a）（x+b）=x2-（a+b）x-ab；
（3）2a2•2a-1=a；
（4）2a3÷（2a3-a2）=1-2a．
其中不成立的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
设边长为2的正方形的对角线长为a，下列关于a的四种说法：
①
是分数；②a可以用数轴上的一个点来表示；③3＜a＜4；④a是8的算术平方根．
其中所有正确说法的序号是（ ）
①
| a |
| 4 |
其中所有正确说法的序号是（ ）
| A、①④ | B、②④ | C、①②④ | D、①③ |
下列各图形都是由同样大小的菱形按一定规律组成的，其中第（1）个图形中菱形的个数是1，第（2）个图形中菱形的个数是5，第（3）个图形中菱形的个数是14，第（4）个图形中菱形的个数是30，…，则第（8）个图形中菱形的个数是（ ）
| A、196 | B、204 |
| C、214 | D、228 |
下列有关
叙述错误的是（ ）
| 3 |
A、
| ||||
B、
| ||||
C、1＜
| ||||
D、
|
边长为4的等边三角形绕它的高所在的直线旋转180°，所得的圆锥的表面积为（ ）
| A、12π | ||
B、（4
| ||
C、（8
| ||
| D、8π |
如图，直线y=-x+3与x轴交于点A，与y轴交于点B，抛物线y=-x2+bx+c经过点A、B．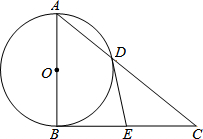
如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC边的中点，连接DE．