题目内容
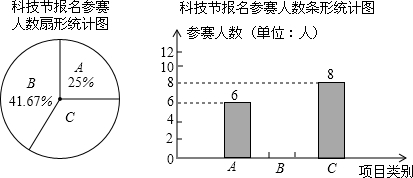
2.如图1,已知:在△ABC中,∠ACB=90°,AC=BC,△ABC内一点P将三个内角分成6个角(即∠1、∠2、∠3、∠4、∠5、∠6)(1)若∠1=∠3=∠5,求S△APC:S△ABC的值;
(2)如图2,已知:AP=AC
①若PB=PC,求证:∠1=2∠4;
②若∠1=30°,求证:PB=PC.
分析 (1)根据等腰直角三角形的性质得到∠CAB=∠ABC=45°.设AC=a,PC=x,证明△APB∽△BPC,根据相似三角形的性质、三角形的面积公式计算即可;
(2)①根据等腰三角形的性质、三角形内角和定理计算;
②过P作PD⊥AC于D,PE⊥BC于E,根据线段垂直平分线的判定定理和性质定理证明.
解答 解:(1)∵AC=BC,∠ACB=90°,
∴∠CAB=∠ABC=45°.
∵∠1=∠3=∠5,
∴∠2=∠4,
∴∠APB=180°-(∠2+∠3)=180°-45°=135°,
同理,∠BPC=135°.
∴∠APC=90°,
设AC=a,PC=x,则AB=$\sqrt{2}$a,
∵∠APB=∠BPC,∠2=∠4,
∴△APB∽△BPC,
∴$\frac{PC}{PB}$=$\frac{PB}{PA}$=$\frac{BC}{AB}$=$\frac{1}{\sqrt{2}}$,
∴PB=$\sqrt{2}$x,PA=2x,
在Rt△PAC中,x2+(2x)2=a2,
∴x2=$\frac{1}{5}$a2,
∵S△APC=$\frac{1}{2}$×x×2x=x2=$\frac{1}{5}$a2,
S△ABC=$\frac{1}{2}$×a×a=$\frac{1}{2}$a2,
∴S△APC:S△ABC=2:5;
(2)①∵PB=PC,则∠4=∠5,
设∠4=∠5=α,
∵AP=AC,则∠6=∠APC=90°-α,即∠1=180°-2(90°-α)=2α,
即∠1=2∠4,
②如图2所示,过P作PD⊥AC于D,PE⊥BC于E,
则四边形PDCE为矩形,
在直角△APD中,∠1=30°,
∴PD=$\frac{1}{2}$PA,
又AP=AC=BC,
∴PD=CE=$\frac{1}{2}$BC,即PE垂直平分BC,
∴PB=PC.
点评 本题考查的是等腰直角三角形的性质、相似三角形的判定和性质、勾股定理、矩形的判定、线段垂直平分线的判定和性质,掌握相关的判定定理和性质定理是解题的关键.

 圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )
圆锥的主视图如图所示(单位:cm),则这个圆锥的侧面积是( )| A. | 15cm2 | B. | 15πcm2 | C. | 30πcm2 | D. | 60cm2 |
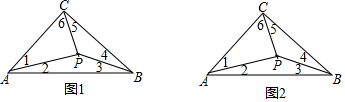
 如图是某校参加各兴趣小组的学生人数分布扇形统计图,由图可知,该校参加人数最多的兴趣小组是( )
如图是某校参加各兴趣小组的学生人数分布扇形统计图,由图可知,该校参加人数最多的兴趣小组是( )| A. | 棋类 | B. | 书画 | C. | 演艺 | D. | 球类 |
| A. | 0.155×104 | B. | 0.155×105 | C. | 1.55×104 | D. | 1.55×105 |
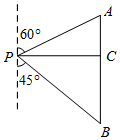 如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.
如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.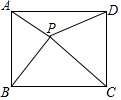 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断: