题目内容
观察下面的5个等式:22=1+12+2,32=2+22+3,42=3+32+4,52=4+42+5,62=5+52+6,…
(1)请你写出第6个等式;
(2)如果用n表示正整数,请你用含有字母n的等式表示你发现的规律,并用所学知识说明所发现的规律的正确性.
(1)请你写出第6个等式;
(2)如果用n表示正整数,请你用含有字母n的等式表示你发现的规律,并用所学知识说明所发现的规律的正确性.
考点:规律型:数字的变化类
专题:
分析:(1)根据已知所反映的规律:等式的左边是序数加1的平方,右边第一个加数是序数,第二个加数是序数的平方,第三个加数是序数加1,由此得出即可.
(2)根据(1)所反映的规律得出,并用n表示,进一步证明即可.
(2)根据(1)所反映的规律得出,并用n表示,进一步证明即可.
解答:解:(1)22=1+12+2,
32=2+22+3,
42=3+32+4,
52=4+42+5,
62=5+52+6,
第6个等式为72=6+62+7;
(2)含有字母n的等式表示为:(n+1)2=n+n2+(n+1),
右边=n+n2+(n+1)=n2+2n+1=(n+1)2=左边.
所以正确.
32=2+22+3,
42=3+32+4,
52=4+42+5,
62=5+52+6,
第6个等式为72=6+62+7;
(2)含有字母n的等式表示为:(n+1)2=n+n2+(n+1),
右边=n+n2+(n+1)=n2+2n+1=(n+1)2=左边.
所以正确.
点评:此题考查数字的变化规律,发现规律,利用规律解决问题.

练习册系列答案
相关题目
 如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点G,过点B作AC的垂线垂足为E,过点C作BC的垂线交BD延长线于点F,当点G为BF的中点时,
如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点G,过点B作AC的垂线垂足为E,过点C作BC的垂线交BD延长线于点F,当点G为BF的中点时,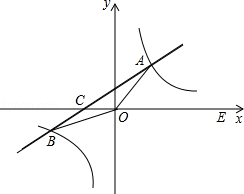 如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=