题目内容
6．已知一元二次方程x2-2mx+m2+m-1=0，其中m为常数，当m变化时，设抛物线的顶点为M，点N的坐标为（3，0），请求出线段MN的最小值．分析 根据题意得出M点坐标，进而利用两点之间距离公式得出MN2最小为2，进而求出答案．
解答 解：由题意可得：y=x2-2mx+m2+m-1=（x-m）2+m-1，
则M（m，m-1），
∵点N的坐标为（3，0），
∴MN2=（3-m）2+（m-1）2=2m2-8m+10=2（m-2）2+2，
故m=2时，MN2最小为2，
则线段MN的最小值为：$\sqrt{2}$．
点评 此题主要考查了二次函数的性质以及两点之间距离公式，得出MN2的最小值是解题关键．
练习册系列答案
相关题目
9．某工程队有14名员工，他们的工种及相应每人每月工资如下表所示：
现该工程队进行了人员调整：减少木工2名，增加电工、瓦工各1名，与调整前相比，该工程队员工月工资的方差变大（填“变小”、“不变”或“变大”）．
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 7000 |
| 木工 | 4 | 6000 |
| 瓦工 | 5 | 5000 |
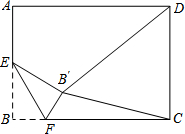如图所示，在矩形ABC中，AB=4，AD=4$\sqrt{2}$，E是线段AB的中点，F是线段BC上的动点，△BEF沿直线EF翻折到△B′EF，连结DB′，B′C．当DB′最短时，则sin∠B′CF=$\frac{\sqrt{3}}{3}$．
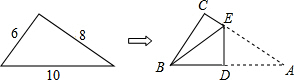如图，一个三角形三边长为6，8，10，现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则CE的长是$\frac{7}{4}$．
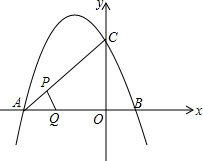如图，二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A，B两点（点B在点A的右侧），与y轴交于点C，若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿线段AC，AB运动，其中一点到达端点时，另一点也随之停止运动．
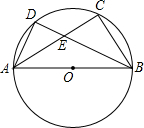如图，AB是⊙O的直径，$\widehat{AD}$=$\widehat{DC}$，AB=10，BD=8，则AE=$\frac{15}{2}$．
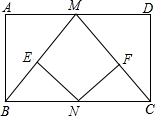如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM的中点．若AB=8，AD=12，则四边形ENFM的周长为20．
如图，△ABC中，CD是边AB上的高，且$\frac{AD}{CD}$=$\frac{CD}{BD}$．