题目内容
6.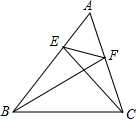 如图,△ABC中,CE⊥AB,BF⊥AC,若∠A=60°,BC=4,则EF的长为2.
如图,△ABC中,CE⊥AB,BF⊥AC,若∠A=60°,BC=4,则EF的长为2.
分析 先判定△AFB∽△AEC,进而证明△AEF∽△ACB,得到$\frac{EF}{CB}$=$\frac{AF}{AB}$,再证明AB=2AF,问题即可解决.
解答 解:∵CE⊥AB,BF⊥AC,
∴∠AFB=∠AEC=90°,
又∵∠A=∠A,
∴△AFB∽△AEC,
∴$\frac{AE}{AF}$=$\frac{AC}{AB}$,即$\frac{AE}{AC}$=$\frac{AF}{AB}$,
又∵∠A=∠A,
∴△AEF∽△ACB,
∴$\frac{EF}{CB}$=$\frac{AF}{AB}$,
∵BF⊥AC,且∠A=60°,
∴∠ABF=30°,
∴AF=$\frac{1}{2}$AB,
∴EF=$\frac{1}{2}$BC=2.
故答案为:2.
点评 该题主要考查了相似三角形的判定及其性质的应用,解题的关键是灵活运用相似三角形的对应边成比例.

练习册系列答案
相关题目
7.下列现象:①用两颗钉子就可以把木条固定在墙上;
②建筑工人砌墙时,经常现在两墙立桩拉线,然后沿着砌墙;
③从A到B架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程;
⑤同等半径下,半圆的周长小于整圆的周长.
其中能体现数学事实“两点之间,线段最短”的是( )
②建筑工人砌墙时,经常现在两墙立桩拉线,然后沿着砌墙;
③从A到B架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程;
⑤同等半径下,半圆的周长小于整圆的周长.
其中能体现数学事实“两点之间,线段最短”的是( )
| A. | ①②③ | B. | ③⑤ | C. | ②④⑤ | D. | ③④⑤ |
1.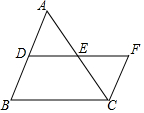 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
 如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△ADE:S四边形BCFD的值为( )| A. | 1:3 | B. | 2:3 | C. | 2:5 | D. | 1:4 |
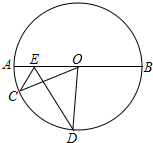 如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD
如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD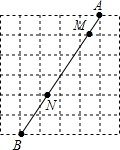 如图,在6×6的正方形网格中,连结两格点A,B,线段AB与网格线的交点为M、N,则AM:MN:NB为1:3:2.
如图,在6×6的正方形网格中,连结两格点A,B,线段AB与网格线的交点为M、N,则AM:MN:NB为1:3:2.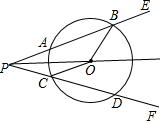 如图,已知点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证:
如图,已知点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证: 如图∠AED=∠C,∠DEF=∠B,试说明∠1+∠2=180°.
如图∠AED=∠C,∠DEF=∠B,试说明∠1+∠2=180°.