题目内容
将抛物线y=x2先向右平移2个单位，再向下平移3个单位，那么得到的新的抛物线的解析式是（ ）
| A、y=（x+2）2+3 |
| B、y=（x+2）2-3 |
| C、y=（x-2）2+3 |
| D、y=（x-2）2-3 |
考点：二次函数图象与几何变换
专题：
分析：先确定出原抛物线的顶点坐标，然后根据向右平移横坐标加，向下平移纵坐标减求出新图象的顶点坐标，然后写出即可．
解答：
解：抛物线y=x2的顶点坐标为（0，0），
向右平移2个单位，再向下平移3个单位后的图象的顶点坐标为（2，-3），
所以，所得图象的解析式为y=（x-2）2-3，
故选：D．
向右平移2个单位，再向下平移3个单位后的图象的顶点坐标为（2，-3），
所以，所得图象的解析式为y=（x-2）2-3，
故选：D．
点评：本题主要考查的是函数图象的平移，根据平移规律“左加右减，上加下减”利用顶点的变化确定图形的变化是解题的关键．
练习册系列答案
相关题目
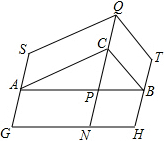如图，△ABC中，∠ACB=90°，分别以它的三边向外作平行四边形，QC∥GS∥TH交AB于P，交GH于N，且QC=PN，若?ABHG和?SQCA的面积分别为8和6，则?QTBC的面积为
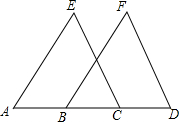已知：如图，点A、B、C、D在同一条直线上，AE∥BF，AE=BF，AB=CD．求证：CE∥DF．若点A（2a-1，5-a）到两坐标轴的距离相等，则点A的坐标是（ ）
| A、（3，3） |
| B、（-9，9） |
| C、（3，3）或（-9，9） |
| D、不确定 |
如图，已知AB∥CD，CE交AB于F，若∠1=50°，则∠C的度数为（ ）| A、40° | B、50° |
| C、60° | D、130° |