题目内容
若m,n为互不相等的两个实数,若2m2-5m-1=0,
+
-2=0.求
+
的值.
| 1 |
| n2 |
| 5 |
| n |
| n |
| m |
| m |
| n |
考点:根与系数的关系
专题:计算题
分析:先把
+
-2=0变形为2n2-5n-1=0,加上2m2-5m-1=0,则可把m、n看作方程2x2-5x-1=0的两根,根据根与系数的关系得到m+n=
,mn=-
,然后把
+
变形为
,再利用整体代入的方法计算.
| 1 |
| n2 |
| 5 |
| n |
| 5 |
| 2 |
| 1 |
| 2 |
| n |
| m |
| m |
| n |
| (m+n)2-2mn |
| mn |
解答:解:∵
+
-2=0.
∴2n2-5n-1=0,
而2m2-5m-1=0,
∴m、n可看作方程2x2-5x-1=0的两根,
∴m+n=
,mn=-
,
∴
+
=
=
=
=-
.
| 1 |
| n2 |
| 5 |
| n |
∴2n2-5n-1=0,
而2m2-5m-1=0,
∴m、n可看作方程2x2-5x-1=0的两根,
∴m+n=
| 5 |
| 2 |
| 1 |
| 2 |
∴
| n |
| m |
| m |
| n |
| m2+n2 |
| mn |
| (m+n)2-2mn |
| mn |
(
| ||||
-
|
| 29 |
| 2 |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
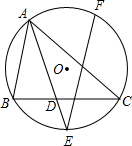 如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.
如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.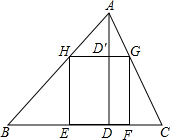 在一底为8米,高为6米的三角形钢板上剪一个面积最大的矩形.
在一底为8米,高为6米的三角形钢板上剪一个面积最大的矩形.