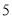��Ŀ����
��ͼ�٣�ƽ��ֱ������ϵXOY�У���A��0��a����B��b��0���ң�a��4��2+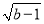 =0����ABΪֱ�DZ�������Rt��ABC����CAB=90�㣬AB=AC��
=0����ABΪֱ�DZ�������Rt��ABC����CAB=90�㣬AB=AC��
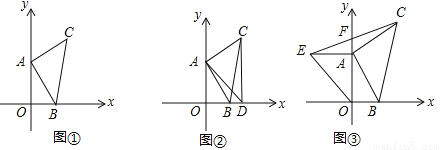
��1����C�����ꣻ
��2����ͼ�ڹ�C����CD��X����D������AD�����ADC�Ķ�����
��3����ͼ���ڣ�1���У���A��Y�����˶�����OAΪֱ�DZ�������Rt��OAE������EC����Y����F������A�����˶�������S��AOB��S��AEF��ֵ�Ƿ�ᷢ���仯�����û�б仯����ֱ��д�����ǵı�ֵ�� ��������Ҫ�����̻�˵�����ɣ���
��1��C������Ϊ��4��5������2����ADC=45�㣻��3��2�� �������������������1����CM��OA��M���ɷǸ��������a=4��b=1����AAS֤����CAM�ա�ABO���ó�MC=OA=4��MA=OB=1�����OM=OA+MA=5�����ɵó�C�����ꣻ ��2��֤��OD=OA���ó���OADΪ����ֱ�������Σ��ó���ADO=45�㣬�����ADC=45�㼴�ɣ� ��3�����жϳ���AEF�ա�MC...
��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
�����Ŀ



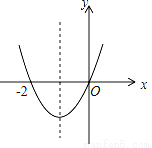
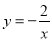 ��ͼ���ϣ���x1��x2��0��x3���������ж�����ȷ���ǣ�������
��ͼ���ϣ���x1��x2��0��x3���������ж�����ȷ���ǣ�������
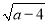 +|b��6|=0����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��C��B��A��O����·�ƶ���
+|b��6|=0����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��C��B��A��O����·�ƶ���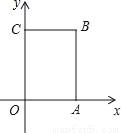
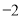 �ĵ�ľ�����
�ĵ�ľ�����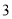 �ĵ��ʾ�����ǣ� ����
�ĵ��ʾ�����ǣ� ����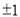 B.
B. 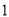 ��
��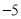 C.
C. 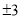 D.
D.