题目内容
15.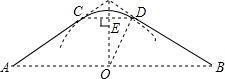 如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.
如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.
分析 连接OC,先根据垂径定理得出DE=$\frac{1}{2}$CD=$\frac{1}{2}$OD,故∠DOE=30°,∠COD=∠DOB=60°,再由弧长公式求出$\widehat{CD}$的长,根据锐角三角函数的定义得出BD的长,进而可得出结论.
解答 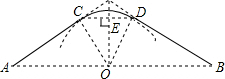 解:∵CD=OD=60米,OE⊥CD,
解:∵CD=OD=60米,OE⊥CD,
∴DE=$\frac{1}{2}$CD=$\frac{1}{2}$OD,
∴∠DOE=30°.
∴∠COD=∠DOB=60°,
∴$\widehat{CD}$=$\frac{60π×60}{180}$=2π(米).
∵AC、BD分别与圆弧CD相切于点C、D,
∴OD⊥BD,
∴BD=OD•tan60°=60×$\sqrt{3}$=60$\sqrt{3}$(米),
∴这条小路的长度=BD+AC+$\widehat{CD}$=60$\sqrt{3}$+60$\sqrt{3}$+2π=(120$\sqrt{3}$+2π)(米).
故答案为:120$\sqrt{3}$+2π.
点评 本题考查的是垂径定理的应用,熟知弧长公式、锐角三角函数的定义、特殊角的三角函数值是解答此题的关键.

练习册系列答案
相关题目
10.一元二次方程x2-6x+8=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
 ____________
____________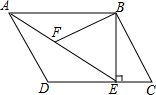 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.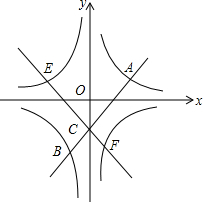 如图,在平面直角坐标系中,双曲线y=$\frac{1}{x}$与一次函数y=kx+b(k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线.若新直线与双曲线y=-$\frac{1}{x}$相交于点E、F,并使得双曲线y=$\frac{1}{x}$,y=-$\frac{1}{x}$,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小.最小值是多少?
如图,在平面直角坐标系中,双曲线y=$\frac{1}{x}$与一次函数y=kx+b(k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线.若新直线与双曲线y=-$\frac{1}{x}$相交于点E、F,并使得双曲线y=$\frac{1}{x}$,y=-$\frac{1}{x}$,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小.最小值是多少?
 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$. 如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.
如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.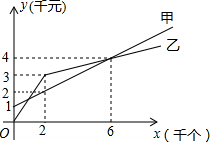 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,