题目内容
6.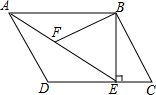 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.(1)△ABF与△ADE相似吗?说说你的理由.
(2)若AB=4,∠BAE=30°,求AE的长.
(3)在(1)、(2)的条件下,若AD=3,求BF的长.
分析 (1)由平行四边形的性质得出∠BAF=∠AED,∠C+∠D=180°,再由已知条件得出∠AFB=∠D,即可得出△ABF∽△ADE;
(2)先证出∠ABE=90°,再运用三角函数即可求出AE;
(3)由△ABF∽△ADE,得出$\frac{BF}{AD}=\frac{AB}{AE}$,即可求出BF.
解答 解:(1)△ABF∽△ADE;理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAF=∠AED,∠C+∠D=180°,
∵∠BFE+∠AFB=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△ADE;
(2)∵AB∥CD,BE⊥CD,
∴BE⊥AB,
∴∠ABE=90°,
∴cos∠BAE=$\frac{AB}{AE}$,
∴AE=$\frac{4}{cos30°}$=$\frac{8\sqrt{3}}{3}$;
(3)∵△ABF∽△ADE,
∴$\frac{BF}{AD}=\frac{AB}{AE}$,
∴BF=$\frac{AD•AB}{AE}$=$\frac{3×4}{\frac{8\sqrt{3}}{3}}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质以及三角函数的运用;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
18.分解因式a2-9a的结果是( )
| A. | a(a-9) | B. | (a-3)(a+3) | C. | (a-3a)(a+3a) | D. | (a-3)2 |
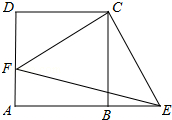 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.
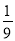 B.
B. 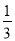 C.
C. 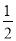 D.
D. 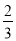
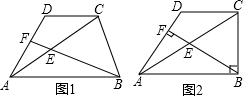 如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.
如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.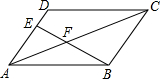 在?ABCD中,E为AD的三等分点,连接BE,交AC于点F,过D作BE的平行线交AC于G,交BC于M,AC=12,则FG为2.4或6.
在?ABCD中,E为AD的三等分点,连接BE,交AC于点F,过D作BE的平行线交AC于G,交BC于M,AC=12,则FG为2.4或6.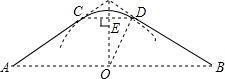 如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.
如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.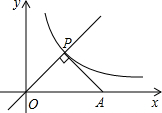 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.