题目内容
 如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.考点:正多边形和圆,相似三角形的判定与性质
专题:
分析:连接BD,构造△DBE,然后证出△DBE∽△FCE,列出
=
,计算FC即可.
| FC |
| BD |
| CE |
| BE |
解答: 解:连接BD.
解:连接BD.
∵CE=
×1=
,
∴BE=
=
,
在Rt△ABD中,BD=
=
,
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴
=
,
∴
=
,
∴FC=
.
 解:连接BD.
解:连接BD.∵CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
(
|
| ||
| 2 |
在Rt△ABD中,BD=
| 12+12 |
| 2 |
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴
| FC |
| BD |
| CE |
| BE |
∴
| FC | ||
|
| ||||
|
∴FC=
| ||
| 5 |
点评:本题考查了正多边形和圆,相似三角形的判定和性质,作出适当辅助线,得到相似三角形是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
三角形外接圆的圆心是三角形的( )
| A、三条高的交点 |
| B、三条边的垂直平分线的交点 |
| C、三个内角的平分线的交点 |
| D、三条边的中线的交点 |
 如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
 如图所示,二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B,交y轴于C,当线段AB最短时,线段OC的长是
如图所示,二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B,交y轴于C,当线段AB最短时,线段OC的长是 如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.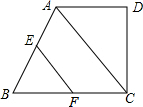 如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=CD,点E,F分别是AB,BD的中点,若EF=2,求CD的值.
如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=CD,点E,F分别是AB,BD的中点,若EF=2,求CD的值. 如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并证明.
如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并证明. 如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.
如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.