题目内容
9.一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.例如:1423,x=1+4,y=2+3,因为x=y,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是1001,最大的“和平数”是9999;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.
例如:1423与4132为一组“相关和平数”
求证:任意的一组“相关和平数”之和是1111的倍数.
分析 (1)根据题意即可得到结论;
(2)设这个“和平数”为$\overline{abcd}$,于是得到d=2a,a+b=c+d,b+c=12k,求得2c+a=12k,即a=2、4,6,8,d=4、8、12(舍去)、16(舍去),①、当a=2,d=4时,2(c+1)=12k,得到c=5则b=7,②、当a=4,d=8时,得到c=4则b=8,于是得到结论;
(3)设任意的两个“相关和平数”为$\overline{abcd}$,$\overline{badc}$(a,b,c,d分别取0,1,2,…,9且a≠0,b≠0),于是得到$\overline{abcd}$+$\overline{badc}$=1100(a+b)+11(c+d)=1111(a+b),即可得到结论.
解答 解:(1)由题意得,最小的“和平数”1001,最大的“和平数”9999,
故答案为:1001,9999;
(2)设这个“和平数”为$\overline{abcd}$,
则d=2a,a+b=c+d,b+c=12k,
∴2c+a=12k,
即a=2、4,6,8,d=4、8、12(舍去)、16(舍去),
①、当a=2,d=4时,2(c+1)=12k,
可知c+1=6k且a+b=c+d,
∴c=5则b=7,
②、当a=4,d=8时,
2(c+2)=12k,
可知c+2=6k且a+b=c+d,
∴c=4则b=8,
综上所述,这个数为2754和4848.
(3)设任意的两个“相关和平数”为$\overline{abcd}$,$\overline{badc}$(a,b,c,d分别取0,1,2,…,9且a≠0,b≠0),
则$\overline{abcd}$+$\overline{badc}$=1100(a+b)+11(c+d)=1111(a+b),
即两个“相关和平数”之和是1111的倍数.
点评 本题考查了因式分解的应用,正确的理解新概念和平数”是解题的关键.

| A. | 已知圆心 | B. | 已知半径 | ||
| C. | 过三个已知点 | D. | 过一个三角形的三个顶点 |
| A型智能手表 | B型智能手表 | |
| 进价 | 1300元/只 | 1500元/只 |
| 售价 | 今年的售价 | 2300元/只 |
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如右表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
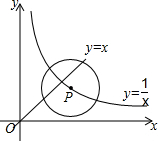 如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )| A. | 1≤x≤$\sqrt{2}$ | B. | $\sqrt{2}-1≤x≤\sqrt{2}$ | C. | $\sqrt{2}-1≤x≤1$ | D. | $\sqrt{2}-1≤x≤\sqrt{2}+1$ |
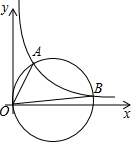 如图,点A(1,2)在反比例函数y=$\frac{k}{x}$(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
如图,点A(1,2)在反比例函数y=$\frac{k}{x}$(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )| A. | (2,1) | B. | (3,$\frac{2}{3}$) | C. | (4,0.5) | D. | (5,0.4) |
| 人数 | 3 | 4 | 8 | 12 | 3 |
| 成绩(次/分钟) | 121 | 157 | 176 | 178 | 184 |
| A. | 175 | B. | 176 | C. | 177 | D. | 178 |
 如图所示,直线l1∥l2,三角尺的一个顶点在l2上,若∠1=70°,则∠2=( )
如图所示,直线l1∥l2,三角尺的一个顶点在l2上,若∠1=70°,则∠2=( )| A. | 70° | B. | 60° | C. | 40° | D. | 30° |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
| x | -3 | -2 | -1 | 0 |
| y | 0 | -3 | -4 | -3 |
①ac<0;
②当x>1时,y随x的增大而增大;
③-4是方程ax2+(b-4)x+c=0的一个根;
④当-1<x<0时,ax2+(b-1)x+c+3>0.其中正确结论的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |