题目内容
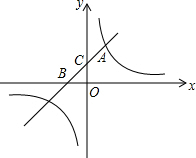 如图,已知一次函数y1=kx+b的图象与反比例函数y2=
如图,已知一次函数y1=kx+b的图象与反比例函数y2=| 8 |
| x |
(1)求点A的坐标;
(2)求一次函数的解析式;
(3)根据图象直接写出当y1>y2时,自变量x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)作AD⊥x轴于点D,则AD∥OC,根据C是AB的中点即可求得D的横坐标,即A的横坐标,代入反比例函数解析式,即可求得纵坐标;
(2)利用待定系数法即可求解;
(3)由两函数交点坐标,利用图形即可得出所求不等式的解集.
(2)利用待定系数法即可求解;
(3)由两函数交点坐标,利用图形即可得出所求不等式的解集.
解答: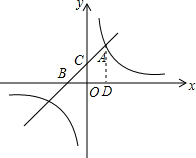 解:(1)作AD⊥x轴于点D,则AD∥OC,
解:(1)作AD⊥x轴于点D,则AD∥OC,
∵C是AB的中点,
∴O是BD的中点.
∵点B的坐标是(-2,0).
∴点D的横坐标是2.
把x=2代入y=
,得y=4,
则A的坐标是(2,4);
(2)点A、B都在直线y=kx+b上,
则
,
解得:
,
则一次函数的解析式是:y=x+2;
(3)根据图象可得:-4<x<0或x>2.
 解:(1)作AD⊥x轴于点D,则AD∥OC,
解:(1)作AD⊥x轴于点D,则AD∥OC,∵C是AB的中点,
∴O是BD的中点.
∵点B的坐标是(-2,0).
∴点D的横坐标是2.
把x=2代入y=
| 8 |
| x |
则A的坐标是(2,4);
(2)点A、B都在直线y=kx+b上,
则
|
解得:
|
则一次函数的解析式是:y=x+2;
(3)根据图象可得:-4<x<0或x>2.
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法与数形结合的数学思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
二次根式
中字母x的取值范围是( )
| x-1 |
| A、x<1 | B、x≤1 |
| C、x>1 | D、x≥1 |
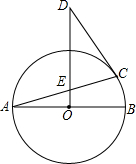 如图,已知AB是⊙O的直径,DO⊥AB于点O,CD是⊙O的切线,切点为C,连接AC,交OD于点E.
如图,已知AB是⊙O的直径,DO⊥AB于点O,CD是⊙O的切线,切点为C,连接AC,交OD于点E.
 如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=
如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=