题目内容
17.在进行二次根式的运算时,如遇到$\frac{2}{\sqrt{3}+1}$这样的式子,还需做进一步的化简:$\frac{2}{\sqrt{3}+1}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-{1}^{2}}$=$\frac{2(\sqrt{3}-1)}{3-1}$=$\sqrt{3}$-1.
还可以用以下方法化简:
$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{(\sqrt{3})^{2}-{1}^{2}}{\sqrt{3}+1}$=$\frac{(\sqrt{3}+1)(\sqrt{3}-1)}{\sqrt{3}+1}$=$\sqrt{3}$-1.
这种化去分母中根号的运算叫分母有理化.
分别用上述两种方法化简:$\frac{2}{\sqrt{5}-\sqrt{3}}$.
分析 根据题中给出的例子把原式进行分母有理化即可.
解答 解:$\frac{2}{\sqrt{5}-\sqrt{3}}$=$\frac{2(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}$=$\frac{2(\sqrt{5}+\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}$=$\frac{2(\sqrt{5}+\sqrt{3})}{2}$=$\sqrt{5}$+$\sqrt{3}$;
或:$\frac{2}{\sqrt{5}-\sqrt{3}}$=$\frac{5-3}{\sqrt{5}-\sqrt{3}}$=$\frac{(\sqrt{5})^{2}-(\sqrt{3})^{2}}{\sqrt{5}-\sqrt{3}}$=$\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}-\sqrt{3}}$=$\sqrt{5}$+$\sqrt{3}$.
点评 本题考查的是分母有理化,分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
相关题目
7.三角形三条中位线的长分别为5、12、13,则此三角形的面积为( )
| A. | 120 | B. | 240 | C. | 30 | D. | 60 |
7.己知点A(3m+1,-2)在第三象限,则m的取值范围是( )
| A. | m<-$\frac{1}{3}$ | B. | m>-$\frac{1}{3}$ | C. | m≤-$\frac{1}{3}$ | D. | m≥-$\frac{1}{3}$ |
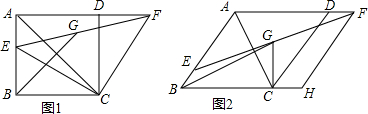
 在?ABCD中,AB=2BC=4,E、F分别为AB、CD的中点
在?ABCD中,AB=2BC=4,E、F分别为AB、CD的中点 如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由.
如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由. 如图所示,抛物线过A、B、C三点,B是C的对称点,顶点为D,与x轴的另一交点为E.
如图所示,抛物线过A、B、C三点,B是C的对称点,顶点为D,与x轴的另一交点为E.